Code
!pip install dldna[colab] # in Colab
# !pip install dldna[all] # in your local“Jede Zahl besteht aus Einheiten, und jede Zahl kann in Einheiten geteilt werden” - Al-Chwarizmi (780-850), persischer Mathematiker
In diesem Kapitel werden wir die mathematischen Konzepte untersuchen, die das Kernstück des Deep Learnings bilden. Deep Learning Modelle bestehen aus einer Kombination komplexer mathematischer Funktionen. Ein tiefes Verständnis von Lineare Algebra, Analysis, Wahrscheinlichkeitstheorie und Statistik ist essentiell, um das Funktionsprinzip der Modelle zu verstehen, die Leistung zu verbessern und neue Modelle zu entwerfen. Zum Beispiel ist ein Verständnis von Matrixoperationen wichtig, um den Funktionsmechanismus von Convolutional Neural Networks (CNN) zu begreifen, während Differentiation und Optimierung eine zentrale Rolle bei der Understanding des Lernprozesses der Modelle spielen.
Falls Sie dieses Kapitel schwierig finden, können Sie zum nächsten Kapitel übergehen. Es ist hilfreich, häufig zurückzukehren und sich mit dem Material vertraut zu machen.
Die lineare Algebra bildet die Fundamente des Deep Learnings. Von Matrixoperationen bis hin zu fortgeschrittenen Optimierungstechniken ist die lineare Algebra ein wesentlicher Werkzeugkasten. In diesem Abschnitt werden wir mit grundlegenden Konzepten wie Vektoren, Matrizen und Tensoren beginnen und uns bis hin zu fortgeschrittenen Themen wie Singulärwertzerlegung und Hauptkomponentenanalyse vorarbeiten.
Vektoren und Matrizen sind die grundlegendsten Operationen, um Daten darzustellen und diese zu transformieren.
Grundlagen von Vektoren
Ein Vektor ist ein mathematisches Objekt, das Größe und Richtung repräsentiert. Die mathematische Definition ist identisch; jedoch kann der Blickwinkel je nach Anwendungsbereich leicht variieren.
In Deep Learning werden Vektoren hauptsächlich verwendet, um verschiedene Merkmale (Features) von Daten gleichzeitig darzustellen. Zum Beispiel kann ein 5-dimensionaler Vektor in einem Modell zur Vorhersage von Hauspreisen wie folgt dargestellt werden:
\(\mathbf{v} = \begin{bmatrix} v_1 \ v_2 \ v_3 \ v_4 \ v_5 \end{bmatrix}\)
Jedes Element dieses Vektors repräsentiert verschiedene Merkmale eines Hauses. \(v_1\): Wohnfläche (Quadratmeter), \(v_2\): Anzahl der Zimmer, \(v_3\): Alter des Hauses (Jahre), \(v_4\): Entfernung zur nächsten Schule (Kilometer), \(v_5\): Kriminalitätsrate (Prozentsatz)
Deep Learning Modelle können solche mehrdimensionalen Vektoren als Eingabe verwenden, um Hauspreise vorherzusagen. Auf diese Weise werden Vektoren verwendet, um die verschiedenen Merkmale komplexer realer Daten effektiv darzustellen und zu verarbeiten.
Vektoren können in NumPy leicht erstellt und verwendet werden.
!pip install dldna[colab] # in Colab
# !pip install dldna[all] # in your localimport numpy as np
# Vector creation
v = np.array([1, 2, 3])
# Vector magnitude (L2 norm)
magnitude = np.linalg.norm(v)
print(f"Vector magnitude: {magnitude}")
# Vector normalization
normalized_v = v / magnitude
print(f"Normalized vector: {normalized_v}")Vector magnitude: 3.7416573867739413
Normalized vector: [0.26726124 0.53452248 0.80178373]Wenn man das Konzept des Vektors genauer betrachtet, gibt es die Unterscheidung zwischen Zeilen- und Spaltenvektoren sowie die Konzepte von kovarianten und kontravarianten Vektoren, die in Physik und Ingenieurwesen verwendet werden.
Zeilen- und Spaltenvektoren
Vektoren werden im Allgemeinen als Spaltenvektoren dargestellt. Zeilenvektoren können als Transponierte (transpose) von Spaltenvektoren angesehen werden. Mathematisch genauer formuliert, kann ein Zeilenvektor auch als Dualvektor oder Kovector bezeichnet werden.
Spaltenvektor: \(\mathbf{v} = \begin{bmatrix} v_1 \ v_2 \ v_3 \end{bmatrix}\), Zeilenvektor: \(\mathbf{v}^T = [v_1 \quad v_2 \quad v_3]\)
Zeilen- und Spaltenvektoren haben unterschiedliche Eigenschaften. Ein Zeilenvektor wirkt als lineare Funktion auf einen Spaltenvektor, um ein Skalar zu erzeugen. Dies wird durch das Skalarprodukt ausgedrückt.
\[\mathbf{u}^T\mathbf{v} = u_1v_1 + u_2v_2 + u_3v_3\]
Kovariante und kontravariante Vektoren
In Physik und Ingenieurwesen sind die Konzepte von kovarianten (covariant vector) und kontravarianten Vektoren (contravariant vector) wichtig. Sie beschreiben das Transformationsverhalten von Vektoren bei Koordinatentransformationen.
In der Tensornotation ist diese Unterscheidung wichtig. Zum Beispiel zeigt \(T^i_j\), dass der obere Index \(i\) kontravarianz und der untere Index \(j\) kovarianz repräsentiert. In der Allgemeinen Relativitätstheorie sind solche Konzepte von kovarianz und kontravarianz besonders wichtig.
Anwendung im Deep Learning
Im Deep Learning wird die Unterscheidung zwischen kovarianz und kontravarianz oft nicht explizit betont. Die Gründe dafür sind:
Trotzdem können diese Konzepte in bestimmten Bereichen, insbesondere in der physikbasierten Maschinelles Lernen oder geometrischen Deep Learning, immer noch wichtig sein. Zum Beispiel spielen die Unterscheidungen zwischen kovarianz und kontravarianz bei Deep-Learning-Modellen, die auf Differentialgeometrie basieren, eine wichtige Rolle in der Modellgestaltung und -interpretation.
Zusammenfassend lässt sich sagen, dass im Deep Learning grundlegende Konzepte von Vektoren vereinfacht verwendet werden. Komplexere mathematische Konzepte spielen jedoch weiterhin eine wichtige Rolle bei fortgeschrittenen Modellierungen und speziellen Anwendungsgebieten.
Der Vektorraum (vector space) ist ein zentrales Konzept der linearen Algebra, das den grundlegenden Rahmen für die Darstellung und Transformation von Daten im Deep Learning bereitstellt. In dieser tiefgehenden Betrachtung schauen wir uns die genaue Definition des Vektorraums sowie verwandte Konzepte an und geben Beispiele für Anwendungen im Deep Learning.
Ein Vektorraum besteht aus einer Menge \(V\) und den Operationen der Addition und Skalarmultiplikation, die 8 Axiome erfüllen. Die Elemente von \(V\) nennt man Vektoren (vectors), und die Skalare sind Elemente der reellen Zahlen \(\mathbb{R}\) oder der komplexen Zahlen \(\mathbb{C}\). (Im Deep Learning werden in der Regel reelle Zahlen verwendet.)
Vektoraddition (Vector Addition): Für beliebige zwei Elemente \(\mathbf{u}, \mathbf{v}\) aus \(V\) ist auch \(\mathbf{u} + \mathbf{v}\) ein Element von \(V\). (Abgeschlossenheit bezüglich der Addition, closed under addition)
Skalarmultiplikation (Scalar Multiplication): Für jedes Element \(\mathbf{u}\) aus \(V\) und einen Skalar \(c\) ist auch \(c\mathbf{u}\) ein Element von \(V\). (Abgeschlossenheit bezüglich der Skalarmultiplikation, closed under scalar multiplication)
Die Vektoraddition und die Skalarmultiplikation müssen die folgenden 8 Axiome erfüllen. (\(\mathbf{u}, \mathbf{v}, \mathbf{w} \in V\), \(c, d\): Skalare)
Beispiele: * \(\mathbb{R}^n\): \(n\)-dimensionaler reeller Vektorraum (n-Tupel von reellen Zahlen) * \(\mathbb{C}^n\): \(n\)-dimensionaler komplexer Vektorraum * \(M_{m \times n}(\mathbb{R})\): \(m \times n\) reeller Matrizenraum * \(P_n\): Raum der Polynome mit reellen Koeffizienten vom Grad \(n\) oder weniger * \(C[a, b]\): Raum der stetigen reellwertigen Funktionen auf dem Intervall \([a, b]\)
Eine Teilmenge \(W\) des Vektorraums \(V\) heißt Teilraum von \(V\), wenn sie folgende Bedingungen erfüllt:
Ein Teilraum ist also eine Teilmenge des Vektorraums, die gleichzeitig selbst die Eigenschaften eines Vektorraums erfüllt.
Für Vektoren \(\mathbf{v}_1, \mathbf{v}_2, ..., \mathbf{v}_k\) aus einem Vektorraum \(V\) und Skalare \(c_1, c_2, ..., c_k\), nennt man einen Ausdruck der Form
\(c_1\mathbf{v}_1 + c_2\mathbf{v}_2 + ... + c_k\mathbf{v}_k\)
eine Linearkombination.
Eine Menge von Vektoren {\(\mathbf{v}_1, \mathbf{v}_2, ..., \mathbf{v}_k\)} heißt linear unabhängig (linearly independent), wenn folgende Bedingung erfüllt ist:
\(c_1\mathbf{v}_1 + c_2\mathbf{v}_2 + ... + c_k\mathbf{v}_k = \mathbf{0}\), dann muss \(c_1 = c_2 = ... = c_k = 0\)
Falls diese Bedingung nicht erfüllt ist (d. h., es existieren Skalare \(c_1, ..., c_k\), die nicht alle Null sind und dennoch obige Gleichung erfüllen), heißt die Menge von Vektoren linear abhängig (linearly dependent).
Intuitiver Sinn:
Eine Menge von Vektoren {\(\mathbf{v}_1, \mathbf{v}_2, ..., \mathbf{v}_k\)} heißt Basis eines Vektorraums \(V\), wenn folgende Bedingungen erfüllt sind: 1. Die Vektoren sind linear unabhängig. 2. Sie spannen den Raum \(V\) auf (siehe unten zur Erklärung von Span).
Die Dimension eines Vektorraums ist die Anzahl der Vektoren in einer Basis des Raums. (dim \(V\))
Kernpunkte: Eine gegebene Basis für einen Vektorraum ist nicht eindeutig, aber jede Basis hat dieselbe Anzahl von Vektoren.
Der Span einer Menge von Vektoren {\(\mathbf{v}_1, \mathbf{v}_2, ..., \mathbf{v}_k\)} ist die Menge aller möglichen Linearkombinationen dieser Vektoren.
span{\(\mathbf{v}_1, \mathbf{v}_2, ..., \mathbf{v}_k\)} = {\(c_1\mathbf{v}_1 + c_2\mathbf{v}_2 + ... + c_k\mathbf{v}_k\) | \(c_1, c_2, ..., c_k\) sind Skalare}
Dies ist die Menge aller Vektoren, die man mit den gegebenen Vektoren erzeugen kann. Der Span bildet immer einen Teilraum. #### Beispiele für Vektorräume im Deep Learning
Das Messen der Größe (magnitude) eines Vektors oder der Distanz zwischen zwei Vektoren ist in Deep Learning sehr wichtig. Es wird in verschiedenen Bereichen wie Verlustfunktionen, Regularisierung, Ähnlichkeitsmaße usw. eingesetzt.
Die Lp-Norm eines Vektors \(\mathbf{x} = [x_1, x_2, ..., x_n]\) wird definiert als (\(p \ge 1\)).
\(||\mathbf{x}||_p = \left( \sum_{i=1}^{n} |x_i|^p \right)^{1/p}\)
Die Distanz zwischen zwei Vektoren \(\mathbf{x}\) und \(\mathbf{y}\) wird in der Regel als die Norm ihrer Differenz definiert.
\(d(\mathbf{x}, \mathbf{y}) = ||\mathbf{x} - \mathbf{y}||\)
Beispiele für Anwendungen im Deep Learning:
Hinweis: In Deep Learning ist es wichtig, “Distanz” und “Ähnlichkeit (similarity)” zu unterscheiden. Je kleiner die Distanz, desto höher die Ähnlichkeit, und je größer die Ähnlichkeit, desto näher liegen die Elemente. Die Cosinus-Ähnlichkeit (cosine similarity) ist eine der häufigsten Methoden zur Bestimmung von Ähnlichkeitsmaßen in Deep Learning.
Ein affiner Raum ist eine Verallgemeinerung des Vektorraums aus der linearen Algebra und dient als nützliches Werkzeug zur geometrischen Interpretation von Deep-Learning-Modellen. Insbesondere repräsentiert die affine Transformation die Form, in der eine lineare Transformation in Deep Learning um einen Bias erweitert wird.
Ein affiner Raum besteht aus einer Struktur mit drei Elementen: (eine Menge von Punkten, ein Vektorraum, die Addition von Punkten und Vektoren). Konkreter:
Diese Addition muss die folgenden beiden Eigenschaften erfüllen:
Wichtige Merkmale
Gegeben sind Punkte \(P_1, P_2, ..., P_k\) in einem affinen Raum \(\mathcal{A}\) und Skalare \(c_1, c_2, ..., c_k\). Eine affine Kombination hat die folgende Form:
\(c_1P_1 + c_2P_2 + ... + c_kP_k\) (mit der Bedingung: \(c_1 + c_2 + ... + c_k = 1\))
Eine affine Transformation ist eine Funktion von einem affinen Raum zu einem anderen und kann als Kombination einer linearen Transformation und einer Translation dargestellt werden. Sie umfasst sowohl eine lineare Transformation als auch einen Bias.
\(f(P) = T(P) + \mathbf{b}\)
Matrizendarstellung:
Eine affine Transformation kann mithilfe einer erweiterten Matrix (augmented matrix) dargestellt werden. In einem \(n\)-dimensionalen affinen Raum können \((n+1)\)-dimensionale Vektoren verwendet werden, um die affine Transformation als eine \((n+1) \times (n+1)\)-Matrix darzustellen. \(\begin{bmatrix} \mathbf{y} \\ 1 \end{bmatrix} = \begin{bmatrix} \mathbf{A} & \mathbf{b} \\ \mathbf{0}^T & 1 \end{bmatrix} \begin{bmatrix} \mathbf{x} \\ 1 \end{bmatrix}\)
In jüngsten Forschungen im Bereich des Deep Learning wurden Modelle vorgeschlagen, die den Bias-Term aufgrund von Berechnungseffizienz, Modellinterpretierbarkeit oder bestimmten theoretischen Grundlagen entfernen.
Gründe für die Entfernung des Bias
Die Konzepte des affinen Raums und der affinen Transformation können für die geometrische Interpretation von Deep-Learning-Modellen, die Analyse der Generalisierungsleistung und das Design neuer Architekturen genutzt werden.
Termini, die mit Tensoren, Vektoren und Matrizen zusammenhängen, werden in der Mathematik, Physik und Informatik etwas unterschiedlich verwendet, was zu Verwirrung führen kann. Um diese Verwirrung zu vermeiden, fassen wir die wichtigsten Konzepte zusammen. Zuerst betrachten wir den Rang und die Dimensionen eines Tensors. Der Rang eines Tensors bezeichnet die Anzahl der Indizes, die der Tensor hat. Zum Beispiel wird ein Skalar als Tensor vom Rang 0, ein Vektor als Tensor vom Rang 1 und eine Matrix als Tensor vom Rang 2 klassifiziert. Tensoren mit drei oder mehr Dimensionen werden allgemein einfach als Tensoren bezeichnet.
Der Begriff “Dimension” kann zwei verschiedene Bedeutungen haben, daher ist Vorsicht geboten. Erstens wird er manchmal im selben Sinne wie der Rang eines Tensors verwendet. In diesem Fall werden Vektoren als eindimensionale Tensoren und Matrizen als zweidimensionale Tensoren bezeichnet. Zweitens wird er auch verwendet, um die Länge oder Größe eines Arrays zu beschreiben. Zum Beispiel ist die Dimension des Vektors \(\mathbf{a} = [1, 2, 3, 4]\) 4.
Es ist wichtig, die Unterschiede in der Verwendung von Begriffen in verschiedenen Bereichen zu kennen. In der Physik wird aufgrund der physikalischen Bedeutung der Anzahl der Elemente tendenziell strenger verwendet. Im Gegensatz dazu werden Vektoren, Matrizen und Tensoren in der Informatik hauptsächlich als Arrays von Zahlen betrachtet, wobei der Begriff “Dimension” sowohl die Anzahl der Daten als auch die Anzahl der Indizes bezeichnet.
Um Verwirrungen durch Unterschiede in der Verwendung von Begriffen zu vermeiden, müssen einige Vorsichtsmaßnahmen beachtet werden. Die Bedeutung eines Begriffs kann je nach Kontext variieren und muss sorgfältig interpretiert werden. Es ist notwendig, klar zwischen den verschiedenen Bedeutungen von “Dimension” in Papieren oder Büchern zu unterscheiden. Insbesondere im Bereich des Deep Learning wird oft sowohl die Anzahl der Daten als auch die Größe des Arrays durch “Dimension” ausgedrückt, daher ist eine konsistente Interpretation wichtig.
In Deep-Learning-Frameworks werden Begriffe wie ‘Dimension’ oder ‘Achse’ verwendet, um die Form (shape) eines Tensors darzustellen. Zum Beispiel kann in PyTorch tensor.shape oder tensor.size() verwendet werden, um die Größe jeder Dimension des Tensors zu überprüfen. In diesem Buch wird der Rang (rank) eines Tensors als ‘Dimension’ bezeichnet und die Länge/Größe eines Arrays als Elementwerte der Form oder als Dimensionen ausgedrückt.
Lassen Sie uns die für das Deep-Learning-Training notwendige Mathematik betrachten. Die lineare Transformation, ein zentrales Rechenverfahren in neuronalen Netzen, wird bei vorwärtsgerichteten Berechnungen sehr einfach dargestellt. In diesem Abschnitt konzentrieren wir uns auf die grundlegende lineare Operation bis hin zur Aktivierungsfunktion.
Die grundlegende Form der vorwärtsgerichteten Operation ist wie folgt gegeben:
\[\boldsymbol y = \boldsymbol x \boldsymbol W + \boldsymbol b\]
Dabei steht \(\boldsymbol x\) für die Eingabe, \(\boldsymbol W\) für die Gewichte, \(\boldsymbol b\) für den Bias und \(\boldsymbol y\) für die Ausgabe. In der Mathematik von neuronalen Netzen werden Eingaben und Ausgaben oft als Vektoren und Gewichte als Matrizen dargestellt. Der Bias (\(\boldsymbol b\)) wird manchmal als Skalarwert dargestellt, muss aber genauer gesagt in der Form eines Vektors, der der Ausgabe entspricht, dargestellt werden.
Matrizen und lineare Transformationen
Matrizen sind ein mächtiges Werkzeug zur Darstellung von linearen Transformationen. Eine lineare Transformation ist ein Prozess, bei dem ein Punkt im Vektorraum auf einen anderen Punkt abgebildet wird, was als Deformation des gesamten Raums angesehen werden kann. Zum besseren visuellen Verständnis dieses Konzepts empfehle ich das Video “Linear transformations and matrices” von 3Blue1Brown[1]. In diesem Video werden die grundlegenden Konzepte der linearen Algebra intuitiv erklärt, und es wird deutlich gezeigt, wie Matrizen den Raum deformieren.
Wenn Eingabedaten \(\boldsymbol x\) als Vektor dargestellt werden, steht dies für einen einzelnen Datensatz, wobei die Länge des Vektors der Anzahl der Merkmale entspricht. In der tatsächlichen Trainingsphase werden jedoch in der Regel mehrere Daten auf einmal verarbeitet. In diesem Fall ist die Eingabe eine Matrix \(\boldsymbol X\) mit der Form (n, m), wobei n die Anzahl der Datensätze und m die Anzahl der Merkmale darstellt.
In realen Deep-Learning-Modellen kann die Eingabedaten nicht nur in einer zweidimensionalen Matrix, sondern auch in höherdimensionalen Tensoren vorliegen.
Um solche hochdimensionale Daten zu verarbeiten, verwenden neuronale Netze verschiedene Arten von linearen und nichtlinearen Transformationen. Im Prozess des Rückwärtspropagierens bei linearer Transformation werden Gradienten berechnet und in umgekehrter Reihenfolge an jede Schicht übertragen, um die Parameter zu aktualisieren. Dieser Prozess kann komplex sein, wird aber durch automatische Differenzierungstools effizient durchgeführt. Die lineare Transformation ist ein grundlegendes Bauteil von Deep-Learning-Modellen, aber die tatsächliche Leistungsfähigkeit der Modelle ergibt sich aus der Kombination mit nichtlinearen Aktivierungsfunktionen. Im nächsten Abschnitt werden wir untersuchen, wie diese Nichtlinearität die Ausdrucksfähigkeit des Modells steigert.
# if in Colab, plase don't run this and below code. just see the result video bleow the following cell.
#from manim import * %%manim -qh -v WARNING LinearTransformations
from manim import *
from manim import config
class LinearTransformations(ThreeDScene):
def construct(self):
self.set_camera_orientation(phi=75 * DEGREES, theta=-45 * DEGREES)
axes = ThreeDAxes(x_range=[-6, 6, 1], y_range=[-6, 6, 1], z_range=[-6, 6, 1], x_length=10, y_length=10, z_length=10).set_color(GRAY)
self.add(axes)
# --- 3D Linear Transformation (Rotation and Shear) ---
title = Text("3D Linear Transformations", color=BLACK).to_edge(UP)
self.play(Write(title))
self.wait(1)
# 1. Rotation around Z-axis
text_rotation = Text("Rotation around Z-axis", color=BLUE).scale(0.7).next_to(title, DOWN, buff=0.5)
self.play(Write(text_rotation))
cube = Cube(side_length=2, fill_color=BLUE, fill_opacity=0.5, stroke_color=WHITE, stroke_width=1)
self.play(Create(cube))
self.play(Rotate(cube, angle=PI/2, axis=OUT, about_point=ORIGIN), run_time=2)
self.wait(1)
self.play(FadeOut(text_rotation))
# 2. Shear
text_shear = Text("Shear Transformation", color=GREEN).scale(0.7).next_to(title, DOWN, buff=0.5)
self.play(Write(text_shear))
# Define the shear transformation matrix. This shears in x relative to y, and in y relative to x.
shear_matrix = np.array([
[1, 0.5, 0],
[0.5, 1, 0],
[0, 0, 1]
])
self.play(
cube.animate.apply_matrix(shear_matrix),
run_time=2,
)
self.wait(1)
# Add transformed axes to visualize the shear
transformed_axes = axes.copy().apply_matrix(shear_matrix)
self.play(Create(transformed_axes), run_time=1)
self.wait(1)
self.play(FadeOut(cube), FadeOut(transformed_axes), FadeOut(text_shear))
# --- 2D to 3D Transformation (Paraboloid) ---
text_2d_to_3d = Text("2D to 3D: Paraboloid", color=MAROON).scale(0.7).next_to(title, DOWN, buff=0.5)
self.play(Write(text_2d_to_3d))
square = Square(side_length=4, fill_color=MAROON, fill_opacity=0.5, stroke_color=WHITE, stroke_width=1)
self.play(Create(square))
def paraboloid(point): # Function for the transformation
x, y, _ = point
return [x, y, 0.2 * (x**2 + y**2)] # Adjust scaling factor (0.2) as needed
paraboloid_surface = always_redraw(lambda: Surface(
lambda u, v: axes.c2p(*paraboloid(axes.p2c(np.array([u,v,0])))),
u_range=[-2, 2],
v_range=[-2, 2],
resolution=(15, 15), # Added for smoothness
fill_color=MAROON,
fill_opacity=0.7,
stroke_color=WHITE,
stroke_width=0.5
).set_shade_in_3d(True))
self.play(
Transform(square, paraboloid_surface),
run_time=3,
)
self.wait(2)
self.play(FadeOut(square), FadeOut(text_2d_to_3d))
# --- 3D to 2D Transformation (Projection) ---
text_3d_to_2d = Text("3D to 2D: Projection", color=PURPLE).scale(0.7).next_to(title, DOWN, buff=0.5)
self.play(Write(text_3d_to_2d))
sphere = Sphere(radius=1.5, fill_color=PURPLE, fill_opacity=0.7, stroke_color=WHITE, stroke_width=1, resolution=(20,20)).set_shade_in_3d(True)
self.play(Create(sphere))
def project_to_2d(mob, alpha):
for p in mob.points:
p[2] *= (1-alpha)
self.play(
UpdateFromAlphaFunc(sphere, project_to_2d),
run_time=2
)
self.wait(1)
# Show a circle representing the final projection
circle = Circle(radius=1.5, color=PURPLE, fill_opacity=0.7, stroke_color = WHITE, stroke_width=1)
self.add(circle)
self.wait(1)
self.play(FadeOut(sphere), FadeOut(text_3d_to_2d), FadeOut(circle), FadeOut(title))
self.wait(1)
import logging
logging.getLogger("manim").setLevel(logging.WARNING)
if __name__ == "__main__":
config.video_dir = "./"
scene = LinearTransformations()
scene.render()Herausforderung: Wie können multidimensionale Daten effizient dargestellt und verarbeitet werden?
Sorgen der Forscher: In den Anfängen des Deep Learnings mussten die Forscher verschiedene Arten von Daten wie Bilder, Texte, Audio usw. bearbeiten. Diese Daten waren schwer als einfache Vektoren oder Matrizen darzustellen und es war notwendig, effektive Methoden zur Verarbeitung komplexer Datenstrukturen zu finden. Darüber hinaus war die Entwicklung von effizienten Berechnungsverfahren zur schnellen Verarbeitung großer Datenmengen eine wichtige Aufgabe.
Tensoren sind grundlegende mathematische Objekte, um Daten und Modellparameter im Deep Learning darzustellen. Sie verallgemeinern das Konzept von Skalaren, Vektoren und Matrizen und können als mehrdimensionale Arrays betrachtet werden. Tensoren werden nach ihren Dimensionen (dimension, rank) wie folgt klassifiziert:
Im Deep Learning werden hauptsächlich die folgenden Formen von Tensoren verwendet:
Die grundlegende lineare Transformation in neuronalen Netzen ist wie folgt:
\(y_j = \sum\limits_{i} x_i w_{ij} + b_j\)
Hierbei ist \(i\) der Index des Inputs und \(j\) der Index des Outputs. Diese Gleichung kann auch in Vektoren- und Matrixform ausgedrückt werden:
\(\boldsymbol x = \begin{bmatrix}x_{1} & x_{2} & \cdots & x_{i} \end{bmatrix}\)
\(\boldsymbol W = \begin{bmatrix} w_{11} & w_{12} & \cdots & w_{1j} \\ w_{21} & w_{22} & \cdots & w_{2j} \\ \vdots & \vdots & \ddots & \vdots \\ w_{i1} & w_{i2} & \cdots & w_{ij} \end{bmatrix}\)
\(\boldsymbol y = \boldsymbol x \boldsymbol W + \boldsymbol b\)
Die wichtigsten Merkmale von Tensoroperationen sind:
Einer der wichtigsten Vorgänge im Lernen von neuronalen Netzen ist die Berechnung von Gradienten. Hauptgradientenberechnungen sind:
Diese Gradienten repräsentieren die Veränderung der Ausgabe in Bezug auf die Veränderungen des Inputs und der Gewichte und sind der Kern des Backpropagation-Algorithmus. Tensoroperationen bilden die Grundlage des modernen Deep Learnings und ermöglichen durch hochgradig parallele Verarbeitung mit GPU das effiziente Training und die Inferenz von großen Modellen. Darüber hinaus ermöglicht die automatische Differenziation (automatic differentiation) von Tensoroperationen effizientes Gradientenrechnen, was zu einem wichtigen Durchbruch in der modernen Deep-Learning-Forschung wurde. Dies geht über einfache numerische Berechnungen hinaus und macht die Struktur und das Lernprozess des Modells zu programmierbaren Objekten. Praktische Beispiele für Tensoroperationen werden wir im dritten Kapitel in PyTorch näher betrachten.
Die Singulärwertzerlegung (Singular Value Decomposition, SVD) und die Hauptkomponentenanalyse (Principal Component Analysis, PCA) sind mächtige mathematische Werkzeuge, die zur Dimensionsreduktion hochdimensionaler Daten und zur Extraktion der wichtigsten Merkmale in den Daten verwendet werden.
SVD ist eine Methode, um eine beliebige \(m \times n\) Matrix \(\mathbf{A}\) als Produkt von drei Matrizen zu zerlegen:
\(\mathbf{A} = \mathbf{U\Sigma V^T}\)
Dabei sind:
Kernideen:
Anwendung in Deep Learning:
Modellkompression: Durch Anwendung der SVD auf Gewichtsmatrizen von neuronalen Netzen kann man diese durch niedrigdimensionale Matrizen approximieren, um die Größe des Modells zu reduzieren und die Inferenzgeschwindigkeit zu verbessern. Insbesondere ist dies effektiv zur Reduzierung der Größe von Embedding-Matrizen in transformerbasierten Sprachmodellen (wie z.B. BERT).
Empfehlungssysteme: SVD kann verwendet werden, um latente Faktoren zwischen Benutzern und Artikeln zu extrahieren.
Die PCA ist eine Methode, die die Daten in Richtungen projiziert, die die Varianz der Daten maximieren (Hauptkomponenten). Sie ist eng mit SVD verwandt und findet die Hauptkomponenten durch Eigenwertzerlegung der Kovarianzmatrix der Daten.
PCA-Schritte: 1. Datenzentrierung (Data Centering): Den Mittelwert jedes Merkmals (Feature) auf 0 setzen. 2. Berechnung der Kovarianzmatrix: Die Kovarianzmatrix, die die Korrelationen zwischen den Merkmalen darstellt, berechnen. 3. Eigenwertzerlegung: Eigenwerte und Eigenvektoren der Kovarianzmatrix berechnen. * Eigenvektoren: Richtungen der Hauptkomponenten * Eigenwerte: Varianz in den jeweiligen Richtungen der Hauptkomponenten 4. Auswahl der Hauptkomponenten: Die ersten \(k\) Eigenvektoren mit den größten Eigenwerten auswählen. (Daten auf \(k\) Dimensionen reduzieren) 5. Datenprojektion: Die Daten auf die ausgewählten \(k\) Hauptkomponenten projizieren, um die Dimensionalität zu reduzieren.
Anwendung im Deep Learning:
SVD vs. PCA
SVD und PCA sind mathematische Werkzeuge, die in Deep Learning eine wichtige Rolle bei der effizienten Darstellung von Daten und der Steigerung der Modellleistung spielen.
from dldna.chapter_02.pca import visualize_pca
visualize_pca()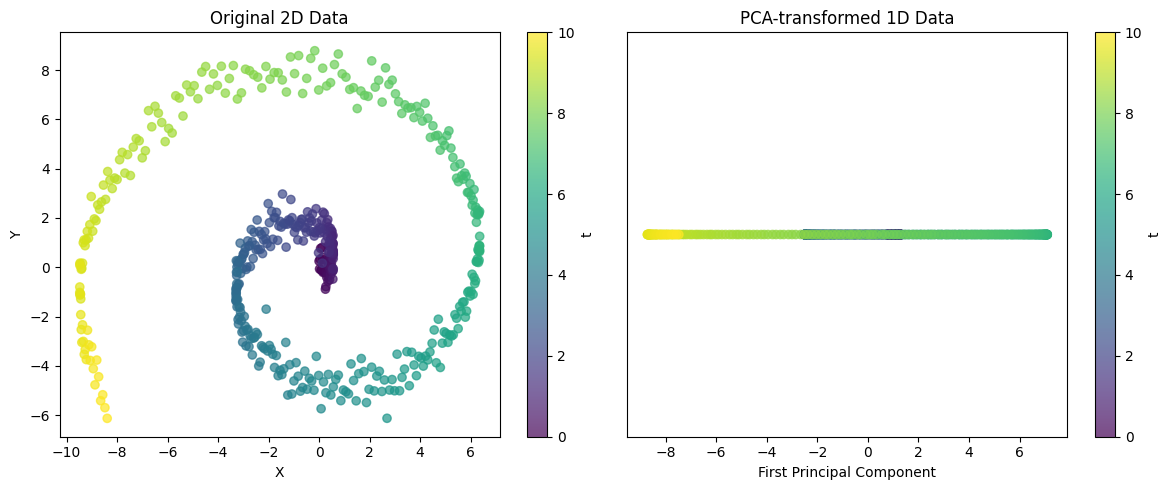
Explained variance ratio: 0.5705Dieses Beispiel zeigt die Fähigkeit der PCA, komplexe 2D-Strukturen in eine 1D-Darstellung zu projizieren. Im Fall von Spiralendaten kann ein einzelnes Hauptkomponente zwar nicht alle Varianz erfassen, aber den wesentlichen Trend der Daten darstellen. Durch den Anteil der erklärteten Varianz kann bewertet werden, wie gut diese 1D-Darstellung die Struktur der ursprünglichen Daten beibehält.
Diese Techniken sind leistungsstarke Werkzeuge zur Extraktion wichtiger Muster aus komplexen Daten.
SVD und PCA sind leistungsstarke Werkzeuge, um wichtige Muster aus hochdimensionalen Daten zu extrahieren und komplexe Datenstrukturen zu vereinfachen.
Herausforderung: Wie kann man die Ableitung komplex verschachtelter Funktionen effizient berechnen?
Sorgen der Forscher: Frühe Deep-Learning-Forscher mussten den Backpropagation-Algorithmus verwenden, um die Gewichte des neuronalen Netzes zu aktualisieren. Da neuronale Netze eine Struktur sind, in der mehrere Schichten von Funktionen komplex miteinander verbunden sind, war es ein sehr schwieriges Problem, die Ableitung der Verlustfunktion nach jedem Gewicht zu berechnen. Insbesondere nahm der Berechnungsaufwand mit der Tiefe der Schichten exponentiell zu und machte das Lernen ineffizient.
Die wichtigste Differentiationsregel im Deep Learning ist die Kettenregel (chain rule). Die Kettenregel ist eine leistungsstarke und elegante Regel, die es ermöglicht, die Ableitung einer zusammengesetzten Funktion als Produkt der Ableitungen ihrer Bestandteile darzustellen. Durch die Visualisierung der Kettenregel kann das Konzept leichter verstanden werden. Nehmen wir zum Beispiel an, \(z\) ist eine Funktion von \(x\) und \(y\), und \(x\) und \(y\) sind jeweils Funktionen von \(s\) und \(t\). Diese Beziehung kann in einem Baumdiagramm dargestellt werden.
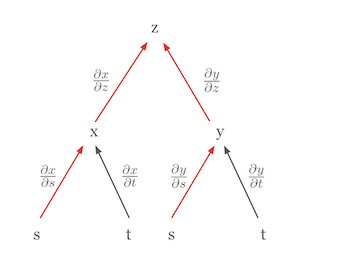
In diesem Diagramm entspricht die partielle Ableitung von \(z\) nach \(s\), \(\frac{\partial z}{\partial s}\), der Summe der Produkte der partiellen Ableitungen entlang aller Pfade von \(z\) zu \(s\).
\(\frac{\partial z}{\partial s} = \frac{\partial z}{\partial x} \frac{\partial x}{\partial s} + \frac{\partial z}{\partial y} \frac{\partial y}{\partial s}\)
In dieser Formel
Nehmen wir als weiteres Beispiel die Darstellung der vollständigen Differentiation mit Hilfe der Kettenregel. Betrachten wir den Fall, dass \(z\) eine Funktion unabhängiger Variablen ist. In diesem Fall vereinfacht sich die Kettenregel zur Form der vollständigen Differentiation. Nehmen wir an, \(z = f(x, y)\) und \(x = g(s)\), \(y = h(t)\), wobei \(s\) und \(t\) unabhängig voneinander sind. Dann kann die vollständige Differentiation von \(z\) wie folgt ausgedrückt werden.
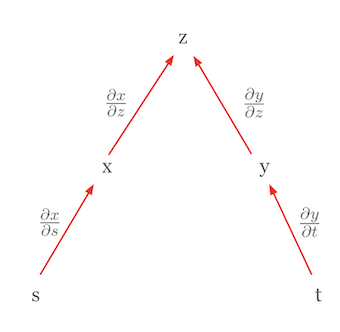
\(dz = \frac{\partial z}{\partial x}dx + \frac{\partial z}{\partial y}dy\)
Hier sind \(dx = \frac{\partial x}{\partial s}ds\) und \(dy = \frac{\partial y}{\partial t}dt\), so dass letztlich die folgende Form entsteht.
\(dz = \frac{\partial z}{\partial x}\frac{\partial x}{\partial s}ds + \frac{\partial z}{\partial y}\frac{\partial y}{\partial t}dt\)
Diese Gleichung sieht similar zur Kettenregel, stellt jedoch tatsächlich eine vollständige Differentiation dar. Ein wichtiger Punkt hierbei ist, dass \(s\) und \(t\) unabhängig voneinander sind, daher \(\frac{\partial x}{\partial t}\) und \(\frac{\partial y}{\partial s}\) null sind. Diese Form ist die der vollständigen Differentiation. Die vollständige Differentiation zeigt den gesamten Einfluss, den Veränderungen aller unabhängigen Variablen auf den Funktionswert haben, und wird durch die Summe der partiellen Ableitungen nach jeder Variable ausgedrückt. Die Struktur der Kettenregel ermöglicht es, die Ableitung komplexer Funktionen in einfachere Teile zu zerlegen. Dies ist besonders wichtig im Deep Learning, da Neuronale Netze eine überlappende Struktur aus mehreren Schichten von Funktionen aufweisen. Mit Hilfe von Baumdiagrammen kann die Kettenregel auch in komplizierteren Situationen leicht angewendet werden. Man beginnt bei der abhängigen Variable, durchläuft alle Wege über die Zwischenvariablen zu den unabhängigen Variablen, multipliziert entlang jedes Pfades die partiellen Ableitungen und addiert dann alle diese Ergebnisse.
Die Kettenregel bildet die mathematische Grundlage des Backpropagation-Algorithmus im Deep Learning. Sie ermöglicht es, die Gewichte komplexer Neuronalen Netze-Modelle effizient zu aktualisieren.
Herausforderung: Wie kann die Differentiation von Funktionen mit verschiedenen Eingabe- und Ausgabeformen verallgemeinert werden?
Forscherfrust: In den Anfängen des Deep Learnings wurden hauptsächlich skalare Funktionen behandelt, aber allmählich mussten auch Funktionen mit Vektoren, Matrizen usw. als Eingabe- und Ausgabeformen verarbeitet werden. Die Darstellung und Berechnung der Differentiation solcher Funktionen auf einheitliche Weise war eine wesentliche Aufgabe bei der Entwicklung von Deep-Learning-Frameworks.
Im Deep Learning werden Funktionen mit verschiedenen Eingabe- (Skalar, Vektor, Matrix, Tensor) und Ausgabeformen (Skalar, Vektor, Matrix, Tensor) behandelt. Dementsprechend ändert sich auch die Darstellung der Ableitung (Differential) der Funktion. Das Kernziel ist es, diese verschiedenen Arten von Ableitungen konsistent darzustellen und durch Anwendung des Kettenregels effizient zu berechnen.
Gradient: Dies ist die Darstellung, die verwendet wird, um eine skalare Funktion nach einem Vektor abzuleiten. Es handelt sich um einen Spaltenvektor, dessen Elemente die partiellen Ableitungen der Funktion nach den einzelnen Komponenten des Eingabevektors sind. Er zeigt die Richtung des steilsten Anstiegs der Funktion.
Jakobimatrix: Dies ist die Darstellung, die verwendet wird, um einen Vektor nach einem Vektor abzuleiten. Es handelt sich um eine Matrix, deren Elemente die partiellen Ableitungen der einzelnen Komponenten des Ausgabevektors nach den einzelnen Komponenten des Eingabevektors sind.
| Eingabeform | Ausgabeform | Ableitungs-Darstellung | Dimension |
|---|---|---|---|
| Vektor (\(\mathbf{x}\)) | Vektor (\(\mathbf{f}\)) | Jakobimatrix (\(\mathbf{J} = \frac{\partial \mathbf{f}}{\partial \mathbf{x}}\)) | \(n \times m\) |
| Matrix (\(\mathbf{X}\)) | Vektor (\(\mathbf{f}\)) | Drei-dimensionaler Tensor (in der Regel nicht gut handhabbar) | - |
| Vektor (\(\mathbf{x}\)) | Matrix (\(\mathbf{F}\)) | Drei-dimensionaler Tensor (in der Regel nicht gut handhabbar) | - |
| Skalar (\(x\)) | Vektor (\(\mathbf{f}\)) | Spaltenvektor (\(\frac{\partial \mathbf{f}}{\partial x}\)) | \(n \times 1\) |
| Vektor (\(\mathbf{x}\)) | Skalar (\(f\)) | Gradient (\(\nabla f = \frac{\partial f}{\partial \mathbf{x}}\)) | \(m \times 1\) (Spaltenvektor) |
| Matrix (\(\mathbf{X}\)) | Skalar (\(f\)) | Matrix (\(\frac{\partial f}{\partial \mathbf{X}}\)) | \(m \times n\) |
Hinweis:
So sind die Konzepte von Gradienten und Jakobimatrizen essentielle Werkzeuge im Deep Learning, um die Differentiation verschiedener Funktionen zu generalisieren und durch Rückpropagation das Modell effizient zu trainieren.
Definition: Die Hesse-Matrix ist eine Darstellung der zweiten partiellen Ableitungen einer skalaren Funktion in Form einer Matrix. Das heißt, wenn die Funktion \(f(x_1, x_2, ..., x_n)\) gegeben ist, wird die Hesse-Matrix \(H\) wie folgt definiert.
\[ H = \begin{bmatrix} \frac{\partial^2 f}{\partial x_1^2} & \frac{\partial^2 f}{\partial x_1 \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_1 \partial x_n} \\ \frac{\partial^2 f}{\partial x_2 \partial x_1} & \frac{\partial^2 f}{\partial x_2^2} & \cdots & \frac{\partial^2 f}{\partial x_2 \partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^2 f}{\partial x_n \partial x_1} & \frac{\partial^2 f}{\partial x_n \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_n^2} \end{bmatrix} \]
Bedeutung:
Der Kern des Lernens von neuronalen Netzen ist der Algorithmus der Rückwärtspropagation (Backpropagation). Die Rückwärtspropagation ist eine effiziente Methode, um den Fehler, der sich im Ausgabeschicht erzeugt hat, in Richtung Eingabeschicht zu verbreiten und dabei die Gewichte und Biases jeder Schicht zu aktualisieren. Dabei ermöglicht die Kettenregel (Chain Rule) die Berechnung komplexer zusammengesetzter Funktionen durch Darstellung als Produkt einfacher Ableitungen.
Neuronale Netze bestehen aus mehreren Schichten, die zusammengefasste Funktionen bilden. Zum Beispiel kann ein zweischichtiges neuronales Netz wie folgt dargestellt werden:
\(\mathbf{z} = f_1(\mathbf{x}; \mathbf{W_1}, \mathbf{b_1})\) \(\mathbf{y} = f_2(\mathbf{z}; \mathbf{W_2}, \mathbf{b_2})\)
Dabei ist \(\mathbf{x}\) die Eingabe, \(\mathbf{z}\) die Ausgabe der ersten Schicht (Eingabe der zweiten Schicht), \(\mathbf{y}\) die endgültige Ausgabe, \(\mathbf{W_1}\), \(\mathbf{b_1}\) die Gewichte und Biases der ersten Schicht, und \(\mathbf{W_2}\), \(\mathbf{b_2}\) die Gewichte und Biases der zweiten Schicht.
Im Prozess der Rückwärtspropagation müssen wir die Gradienten des Verlustfunktion \(E\) für jedes Parameter (\(\frac{\partial E}{\partial \mathbf{W_1}}\), \(\frac{\partial E}{\partial \mathbf{b_1}}\), \(\frac{\partial E}{\partial \mathbf{W_2}}\), \(\frac{\partial E}{\partial \mathbf{b_2}}\)) berechnen. Hierbei kann die Kettenregel wie folgt angewendet werden:
\(\frac{\partial E}{\partial \mathbf{W_2}} = \frac{\partial E}{\partial \mathbf{y}} \frac{\partial \mathbf{y}}{\partial \mathbf{W_2}}\) \(\frac{\partial E}{\partial \mathbf{b_2}} = \frac{\partial E}{\partial \mathbf{y}} \frac{\partial \mathbf{y}}{\partial \mathbf{b_2}}\) \(\frac{\partial E}{\partial \mathbf{W_1}} = \frac{\partial E}{\partial \mathbf{y}} \frac{\partial \mathbf{y}}{\partial \mathbf{z}} \frac{\partial \mathbf{z}}{\partial \mathbf{W_1}}\) \(\frac{\partial E}{\partial \mathbf{b_1}} = \frac{\partial E}{\partial \mathbf{y}} \frac{\partial \mathbf{y}}{\partial \mathbf{z}} \frac{\partial \mathbf{z}}{\partial \mathbf{b_1}}\)
Auf diese Weise kann die Kettenregel verwendet werden, um die Gradienten komplexer neuronalen Netze in einer Kette von Produkten einfacher Ableitungen zu zerlegen und effizient zu berechnen. Die Theorie-Vertiefung 2.2.4 erklärt diesen Prozess detaillierter.
Basierend auf diesen Konzepten, werden wir im nächsten Abschnitt detailliert die Berechnung von Gradienten während des Rückpropagationsprozesses anhand konkreter Beispiele betrachten.
Der Kern des Backpropagation-Algorithmus besteht darin, die Gradienten der Verlustfunktion (Loss Function) zu berechnen und Gewichte entsprechend zu aktualisieren. Als Beispiel betrachten wir eine einfache lineare Transformation (\(\mathbf{y} = \mathbf{xW} + \mathbf{b}\)), um den Backpropagation-Prozess zu erläutern.
Backpropagation ist ein Algorithmus, der die Fehler am Ausgabeschicht in Richtung Eingangsschicht propagiert und dabei die Gewichte entsprechend dem Beitrag an den Fehlern aktualisiert. Der zentrale Schritt dieses Prozesses besteht darin, die Gradienten der Verlustfunktion nach jedem Gewicht zu berechnen.
Wenn als Verlustfunktion der mittlere quadratische Fehler (Mean Squared Error, MSE) verwendet wird, dann ist der Gradient der Verlustfunktion \(E\) bezüglich des Outputs \(\mathbf{y}\) wie folgt definiert:
\(E = \frac{1}{M} \sum_{i=1}^{M} (y_i - \hat{y}_i)^2\)
\(\frac{\partial E}{\partial \mathbf{y}} = \frac{2}{M}(\mathbf{y} - \hat{\mathbf{y}})\)
Dabei ist \(y_i\) der tatsächliche Wert, \(\hat{y}_i\) der vorhergesagte Wert des Modells und \(M\) die Anzahl der Datenpunkte.
Indem wir die Kettenregel anwenden, können wir den Gradienten der Verlustfunktion \(E\) bezüglich der Gewichte \(\mathbf{W}\) berechnen:
\(\frac{\partial E}{\partial \mathbf{W}} = \frac{\partial E}{\partial \mathbf{y}} \frac{\partial \mathbf{y}}{\partial \mathbf{W}}\)
Da \(\mathbf{y} = \mathbf{xW} + \mathbf{b}\), ist \(\frac{\partial \mathbf{y}}{\partial \mathbf{W}} = \mathbf{x}^T\).
Schließlich kann der Gradient bezüglich der Gewichte wie folgt ausgedrückt werden:
\(\frac{\partial E}{\partial \mathbf{W}} = \mathbf{x}^T \frac{\partial E}{\partial \mathbf{y}}\)
Der Gradient der Verlustfunktion \(E\) bezüglich der Eingabe \(\mathbf{x}\) wird verwendet, um den Fehler auf die vorherige Schicht zu propagieren:
\(\frac{\partial E}{\partial \mathbf{x}} = \frac{\partial E}{\partial \mathbf{y}} \frac{\partial \mathbf{y}}{\partial \mathbf{x}}\)
Da \(\mathbf{y} = \mathbf{xW} + \mathbf{b}\), ist \(\frac{\partial \mathbf{y}}{\partial \mathbf{x}} = \mathbf{W}^T\).
Somit ist der Gradient bezüglich der Eingabe wie folgt definiert:
\(\frac{\partial E}{\partial \mathbf{x}} = \frac{\partial E}{\partial \mathbf{y}} \mathbf{W}^T\)
Backpropagation erfolgt durch die folgenden zentralen Schritte: 1. Vorwärtspropagation (Forward Propagation): Eingabedaten \(\mathbf{x}\) durch das Neuronale Netzwerk leiten, um die Vorhersage \(\hat{\mathbf{y}}\) zu berechnen. 2. Verlustfunktion Berechnung: Die Vorhersage \(\hat{\mathbf{y}}\) mit den tatsächlichen Werten \(\mathbf{y}\) vergleichen und den Verlust \(E\) berechnen. 3. Rückwärtspropagation (Backward Propagation): * Den Gradient der Verlustfunktion am Ausgabeschicht \(\frac{\partial E}{\partial \mathbf{y}}\) berechnen. * Die Kettenregel verwenden, um den Gradient bezüglich der Gewichte zu berechnen: \(\frac{\partial E}{\partial \mathbf{W}} = \mathbf{x}^T \frac{\partial E}{\partial \mathbf{y}}\). * Den Gradient bezüglich der Eingabe \(\frac{\partial E}{\partial \mathbf{x}} = \frac{\partial E}{\partial \mathbf{y}} \mathbf{W}^T\) berechnen, um den Fehler zur vorherigen Schicht weiterzuleiten. 4. Gewichtsaktualisierung: Die berechneten Gradienten verwenden, um die Gewichte durch Optimierungsverfahren wie Gradientendescent zu aktualisieren.
Der Backpropagation-Algorithmus ist der Kern des Lernprozesses von Deep-Learning-Modellen und ermöglicht es, komplexe nichtlineare Funktionen effektiv zu approximieren.
Die Kernidee des Rückpropagationsalgorithmus besteht darin, die Gradienten der Verlustfunktion (Loss Function) zu berechnen, um die Gewichte zu aktualisieren. Als Beispiel betrachten wir den Prozess der Rückpropagation anhand einer einfachen linearen Transformation (\(\mathbf{y} = \mathbf{xW} + \mathbf{b}\)). Hier wird der Berechnungsprozess so detailliert wie möglich erläutert.
Das Ziel des Lernens in neuronalen Netzen ist es, die Verlustfunktion \(E\) zu minimieren. Bei Verwendung des mittleren quadratischen Fehlers (MSE) als Verlustfunktion sieht dies wie folgt aus:
\(E = f(\mathbf{y}) = \frac{1}{M} \sum_{i=1}^{M} (y_i - \hat{y}_i)^2\)
Dabei ist \(y_i\) der tatsächliche Wert, \(\hat{y}_i\) der vorhergesagte Wert und \(M\) die Anzahl der Datenpunkte (oder die Dimension des Ausgabevektors).
Die Ableitung von \(E\) nach \(\mathbf{y}\) lautet wie folgt:
\(\frac{\partial E}{\partial \mathbf{y}} = \frac{2}{M} (\mathbf{y} - \hat{\mathbf{y}})\)
Dabei ist \(\mathbf{y}\) der Ausgabevektor des neuronalen Netzes und \(\hat{\mathbf{y}}\) der Vektork der tatsächlichen Werte (Targets). Da \(y_i\) eine Konstante (jedes Element des Targets) ist, bleibt nur die partielle Ableitung nach \(\mathbf{y}\).
Hinweis: Im Beispielcode aus Kapitel 1 wurde der Term \(-\frac{2}{M}\) verwendet, da die Verlustfunktion in ihrer Definition ein negatives Vorzeichen (-) enthielt. Hier wird die allgemeine MSE-Definition verwendet, daher wird der positive Wert \(\frac{2}{M}\) benutzt. Bei tatsächlichen Lernprozessen wird mit dem Lernrate (learning rate) multipliziert, so dass die genaue Größe dieser Konstanten nicht entscheidend ist.
Nun berechnen wir den Gradienten der Verlustfunktion \(E\) nach den Gewichten \(\mathbf{W}\). Es gilt: \(E = f(\mathbf{y})\) und \(\mathbf{y} = \mathbf{xW} + \mathbf{b}\). Dabei ist \(\mathbf{x}\) der Eingabevektor, \(\mathbf{W}\) die Gewichtsmatrix und \(\mathbf{b}\) der Bias-Vektor.
Berechnungsgraph:
Um den Prozess der Rückpropagation visuell darzustellen, kann ein Berechnungsgraph verwendet werden. (Einfügen eines Bildes des Berechnungsgraphen)
\(E\) ist ein Skalarwert und für jedes \(w_{ij}\) (jedes Element der Gewichtsmatrix \(\mathbf{W}\)) muss die partielle Ableitung von \(E\) berechnet werden. \(\mathbf{W}\) ist eine Matrix mit den Dimensionen (Eingabedimension) x (Ausgabedimension). Zum Beispiel, wenn die Eingabe 3-dimensional (\(x_1, x_2, x_3\)) und die Ausgabe 2-dimensional (\(y_1, y_2\)) ist, sieht die Matrix wie folgt aus:
\(\frac{\partial E}{\partial \mathbf{W}} = \begin{bmatrix} \frac{\partial E}{\partial w_{11}} & \frac{\partial E}{\partial w_{12}} \\ \frac{\partial E}{\partial w_{21}} & \frac{\partial E}{\partial w_{22}} \\ \frac{\partial E}{\partial w_{31}} & \frac{\partial E}{\partial w_{32}} \end{bmatrix}\)
Die Ableitung von \(E\) nach \(\mathbf{y}\) kann als Zeilenvektor \(\frac{\partial E}{\partial \mathbf{y}} = \begin{bmatrix} \frac{\partial E}{\partial y_1} & \frac{\partial E}{\partial y_2} \end{bmatrix}\) dargestellt werden (molekulare Notation). Streng genommen sollte der Gradient als Spaltenvektor dargestellt werden, hier wird jedoch zur Vereinfachung des Rechnens ein Zeilenvektor verwendet.
Gemäß der Kettenregel: \(\frac{\partial E}{\partial \mathbf{W}} = \frac{\partial E}{\partial \mathbf{y}} \frac{\partial \mathbf{y}}{\partial \mathbf{W}}\)
\(\frac{\partial E}{\partial w_{ij}} = \sum_k \frac{\partial E}{\partial y_k} \frac{\partial y_k}{\partial w_{ij}}\) (hierbei ist \(k\) der Index des Ausgabevektors \(\mathbf{y}\))
Die obige Gleichung aufgeschlüsselt:
\(\frac{\partial E}{\partial \mathbf{W}} = \frac{\partial E}{\partial y_1} \frac{\partial y_1}{\partial \mathbf{W}} + \frac{\partial E}{\partial y_2} \frac{\partial y_2}{\partial \mathbf{W}}\)
Nun müssen wir \(\frac{\partial y_k}{\partial w_{ij}}\) berechnen. Da \(\mathbf{y} = \mathbf{xW} + \mathbf{b}\) gilt,
\(y_1 = x_1w_{11} + x_2w_{21} + x_3w_{31} + b_1\) \(y_2 = x_1w_{12} + x_2w_{22} + x_3w_{32} + b_2\)
\(\frac{\partial y_1}{\partial w_{ij}} = \begin{bmatrix} \frac{\partial y_1}{\partial w_{11}} & \frac{\partial y_1}{\partial w_{12}} \\ \frac{\partial y_1}{\partial w_{21}} & \frac{\partial y_1}{\partial w_{22}} \\ \frac{\partial y_1}{\partial w_{31}} & \frac{\partial y_1}{\partial w_{32}} \end{bmatrix} = \begin{bmatrix} x_1 & 0 \\ x_2 & 0 \\ x_3 & 0 \end{bmatrix}\)
\(\frac{\partial y_2}{\partial w_{ij}} = \begin{bmatrix} 0 & x_1 \\ 0 & x_2 \\ 0 & x_3 \end{bmatrix}\)
Folglich,
\(\frac{\partial E}{\partial \mathbf{W}} = \frac{\partial E}{\partial y_1} \begin{bmatrix} x_1 & 0 \\ x_2 & 0 \\ x_3 & 0 \end{bmatrix} + \frac{\partial E}{\partial y_2} \begin{bmatrix} 0 & x_1 \\ 0 & x_2 \\ 0 & x_3 \end{bmatrix} = \begin{bmatrix} \frac{\partial E}{\partial y_1}x_1 & \frac{\partial E}{\partial y_2}x_1 \\ \frac{\partial E}{\partial y_1}x_2 & \frac{\partial E}{\partial y_2}x_2 \\ \frac{\partial E}{\partial y_1}x_3 & \frac{\partial E}{\partial y_2}x_3 \end{bmatrix} = \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} \begin{bmatrix} \frac{\partial E}{\partial y_1} & \frac{\partial E}{\partial y_2} \end{bmatrix} = \mathbf{x}^T \frac{\partial E}{\partial \mathbf{y}}\)
Verallgemeinerung:
Falls die Eingabe ein \(1 \times m\) Zeilenvektor \(\mathbf{x}\) und die Ausgabe ein \(1 \times n\) Zeilenvektor \(\mathbf{y}\) ist, dann ist das Gewicht \(\mathbf{W}\) eine \(m \times n\) Matrix. In diesem Fall, \(\frac{\partial E}{\partial \mathbf{W}} = \mathbf{x}^T \frac{\partial E}{\partial \mathbf{y}}\)
Der Gradient der Verlustfunktion \(E\) nach dem Input \(\mathbf{x}\) kann ebenfalls mit der Kettenregel berechnet werden.
\(\frac{\partial E}{\partial \mathbf{x}} = \frac{\partial E}{\partial \mathbf{y}} \frac{\partial \mathbf{y}}{\partial \mathbf{x}}\)
Da \(\mathbf{y} = \mathbf{xW} + \mathbf{b}\), ist \(\frac{\partial \mathbf{y}}{\partial \mathbf{x}} = \mathbf{W}^T\).
Daher,
\(\frac{\partial E}{\partial \mathbf{x}} = \frac{\partial E}{\partial \mathbf{y}} \mathbf{W}^T\)
Der Gradient der Verlustfunktion nach dem Bias \(\mathbf{b}\) ist wie folgt:
\(\frac{\partial E}{\partial \mathbf{b}} = \frac{\partial E}{\partial \mathbf{y}} \frac{\partial \mathbf{y}}{\partial \mathbf{b}}\)
Da \(\mathbf{y} = \mathbf{xW} + \mathbf{b}\), ist \(\frac{\partial \mathbf{y}}{\partial \mathbf{b}} = \begin{bmatrix} 1 & 1 & \dots & 1\end{bmatrix}\) (ein \(1 \times n\) Zeilenvektor, der nur aus Einsen besteht)
\(\frac{\partial E}{\partial \mathbf{b}} = \frac{\partial E}{\partial \mathbf{y}}\)
Through this mathematical process, deep learning models can learn complex nonlinear transformations from input data to output data.
Deep Learning basiert tiefgehend auf der Wahrscheinlichkeits- und Statistiktheorie, die Unsicherheiten in Daten handhabt. In diesem Kapitel werden wir grundlegende Konzepte wie Wahrscheinlichkeitsverteilungen, Erwartungswerte, Bayes-Theorem und Maximum-Likelihood-Schätzung betrachten. Diese Konzepte sind essentiell für das Verständnis von Lern- und Inferenzprozessen in Modellen.
Herausforderung: Wie kann die Unsicherheit realer Daten mathematisch modelliert werden?
Sorgen der Forscher: Frühe Machine-Learning-Forscher erkannten, dass reale Welt-Daten nicht durch deterministische Regeln erklärt werden können. Dies liegt daran, dass in den Daten Messfehler, Rauschen und unberechenbare Schwankungen vorhanden sind. Es war ein mathematisches Werkzeug erforderlich, um diese Unsicherheit zu quantifizieren und im Modell widerzuspiegeln.
Wahrscheinlichkeitsverteilungen repräsentieren alle möglichen Ausgänge und ihre Auftretenswahrscheinlichkeiten. Sie können in diskrete Wahrscheinlichkeitsverteilungen und stetige Wahrscheinlichkeitsverteilungen unterteilt werden.
Diskrete Wahrscheinlichkeitsverteilungen beziehen sich auf den Fall, in dem die Werte, die eine Zufallsvariable annehmen kann, endlich oder abzählbar sind. Ein charakteristisches Merkmal ist, dass jedem möglichen Ergebnis eine klare Wahrscheinlichkeit zugeordnet werden kann.
Mathematisch wird eine diskrete Wahrscheinlichkeitsverteilung durch die Wahrscheinlichkeitsfunktion (PMF) dargestellt.
\[P(X = x) = p(x)\]
Hierbei ist ( p(x) ) die Wahrscheinlichkeit, dass ( X ) den Wert ( x ) annimmt. Die wesentlichen Eigenschaften sind wie folgt:
Beispiele für diskrete Wahrscheinlichkeitsverteilungen sind die Bernoulli-Verteilung, die Binomialverteilung und die Poisson-Verteilung.
Die Wahrscheinlichkeitsfunktion für das Werfen eines Würfels ist wie folgt:
\[P(X = x) = \begin{cases} \frac{1}{6} & \text{if } x \in \{1, 2, 3, 4, 5, 6\} \\ 0 & \text{otherwise} \end{cases}\]
Diskrete Wahrscheinlichkeitsverteilungen werden in der Maschinelles Lernen und Deep Learning in verschiedenen Bereichen wie Klassifizierungsprobleme, Reinforcement Learning und Natürlichsprachverarbeitung eingesetzt. Das folgende ist das Ergebnis einer Simulation des Würfels werfens.
from dldna.chapter_02.statistics import simulate_dice_roll
simulate_dice_roll()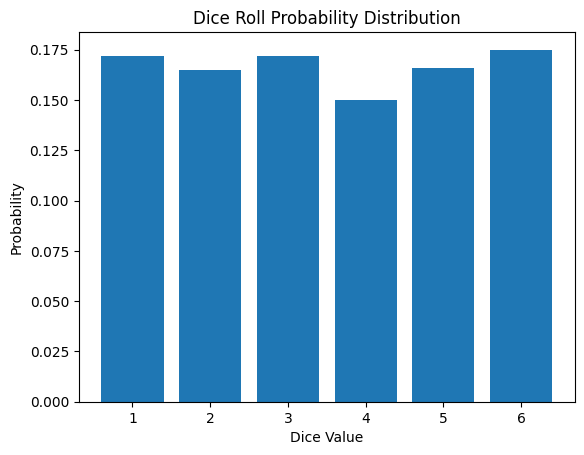
Kontinuierliche Wahrscheinlichkeitsverteilungen behandeln den Fall, dass eine Zufallsvariable kontinuierliche Werte annehmen kann. Im Gegensatz zu diskreten Wahrscheinlichkeitsverteilungen ist die Wahrscheinlichkeit an einem bestimmten Punkt 0 und es wird auf Intervalle angewendet. Mathematisch wird eine kontinuierliche Wahrscheinlichkeitsverteilung durch eine Wahrscheinlichkeitsdichtefunktion (Probability Density Function, PDF) dargestellt.
\[f(x) = \lim_{\Delta x \to 0} \frac{P(x < X \leq x + \Delta x)}{\Delta x}\]
Hierbei stellt ( f(x) ) die Wahrscheinlichkeitsdichte in der Nähe von ( x ) dar. Die wichtigsten Eigenschaften sind wie folgt:
Beispiele dafür sind die Normalverteilung, die Exponentialverteilung und die Gamma-Verteilung.
Die Wahrscheinlichkeitsdichtefunktion der Normalverteilung lautet wie folgt:
\[f(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}\]
Hierbei ist ( ) der Mittelwert und ( ) die Standardabweichung.
Kontinuierliche Wahrscheinlichkeitsverteilungen werden in verschiedenen Anwendungen des Maschinelles Lernens und Deep Learnings, wie Regressionen, Signalverarbeitung und Zeitreihenanalyse, wichtig eingesetzt.
from dldna.chapter_02.statistics import plot_normal_distribution
plot_normal_distribution()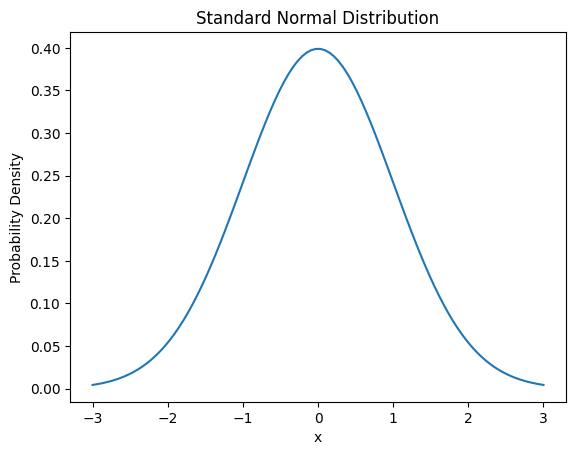
Der Erwartungswert ist ein wichtiges Konzept, das die zentrale Tendenz einer Wahrscheinlichkeitsverteilung darstellt. Dies kann als gewichteter Mittelwert aller möglichen Werte der Zufallsvariable interpretiert werden. Im Fall einer diskreten Wahrscheinlichkeitsverteilung wird der Erwartungswert wie folgt berechnet:
\[E[X] = \sum_{i} x_i P(X = x_i)\]
Hierbei ist \(x_i\) ein möglicher Wert der Zufallsvariable X und \(P(X = x_i)\) die Wahrscheinlichkeit dieses Werts. Im Fall einer stetigen Wahrscheinlichkeitsverteilung wird der Erwartungswert durch Integration berechnet.
\[E[X] = \int_{-\infty}^{\infty} x f(x) dx\]
Hierbei ist \(f(x)\) die Wahrscheinlichkeitsdichtefunktion. Der Erwartungswert hat folgende wichtige Eigenschaften:
Im Deep Learning wird der Erwartungswert bei der Minimierung von Verlustfunktionen oder zur Schätzung von Modellparametern zentral verwendet. Zum Beispiel ist der mittlere quadratische Fehler (MSE) wie folgt definiert:
\[MSE = E[(Y - \hat{Y})^2]\]
Hierbei ist \(Y\) der wahre Wert und \(\hat{Y}\) der vorhergesagte Wert.
Das Konzept des Erwartungswerts bildet die theoretische Grundlage von Optimierungsalgorithmen wie dem stochastischen Gradientenabstieg (Stochastic Gradient Descent) und wird auch bei der Schätzung von Wertfunktionen im Reinforcement Learning wichtig eingesetzt.
from dldna.chapter_02.statistics import calculate_dice_expected_value
calculate_dice_expected_value()Expected value of dice roll: 3.5Diese grundlegenden Konzepte der Wahrscheinlichkeit und Statistik spielen eine zentrale Rolle bei der Gestaltung, dem Lernen und der Evaluation von Deep-Learning-Modellen. Im nächsten Abschnitt werden wir auf dieser Basis den Bayes’schen Satz und die Maximum-Likelihood-Schätzung untersuchen.
Herausforderung: Wie kann man die Parameter eines Modells bei begrenzten Daten am besten schätzen?
Kopfschmerzen des Forschers: Frühe Statistiker und Maschinelles Lernen-Forscher waren oft gezwungen, Modelle mit begrenzten Daten zu erstellen. Die genaue Schätzung von Modellparametern bei unzureichenden Daten war ein sehr schwieriges Problem. Es war notwendig, Methoden zu entwickeln, um die Genauigkeit der Schätzungen durch die Nutzung vorheriger Kenntnisse oder Überzeugungen zu verbessern, anstatt sich nur auf die Daten zu stützen.
Das Bayes-Theorem und die Maximum-Likelihood-Schätzung sind zentrale Konzepte der Wahrscheinlichkeitstheorie und Statistik, die in der Tiefenlernen weithin zur Modellierung und Inferenz angewendet werden.
Das Bayes-Theorem bietet eine Methode zur Berechnung bedingter Wahrscheinlichkeiten. Es wird verwendet, um die Wahrscheinlichkeit einer Hypothese zu aktualisieren, wenn neue Beweise vorliegen. Die mathematische Formulierung des Bayes-Theorems lautet wie folgt:
\[P(A|B) = \frac{P(B|A)P(A)}{P(B)}\]
Dabei: - \(P(A|B)\) ist die Wahrscheinlichkeit von A, gegeben B (Posterior-Wahrscheinlichkeit) - \(P(B|A)\) ist die Wahrscheinlichkeit von B, gegeben A (Likelihood) - \(P(A)\) ist die Wahrscheinlichkeit von A (Prior-Wahrscheinlichkeit) - \(P(B)\) ist die Wahrscheinlichkeit von B (Evidence)
Das Bayes-Theorem wird in der Maschinelles Lernen wie folgt verwendet:
Die Maximum-Likelihood-Schätzung (Maximum Likelihood Estimation, MLE) ist eine Methode, um die Modellparameter zu finden, die die gegebenen Daten am besten erklären. Im Kontext des Tiefenlernens bedeutet dies, dass ein neuronales Netzwerk die Gewichte und Verzerrungen findet, die die beobachteten Daten am besten erklären. Die Maximum-Likelihood-Schätzung sucht also nach den Parametern, die die Wahrscheinlichkeit maximieren, dass das Modell die Trainingsdaten erzeugt hat, was direkt mit dem Lernprozess des Modells verbunden ist.
Die Likelihood-Funktion \(L(\theta|X)\) gibt an, wie wahrscheinlich es ist, die Daten \(X\) bei gegebenen Parametern \(\theta\) zu beobachten. Die mathematische Formulierung der Maximum-Likelihood-Schätzung lautet:
\[\hat{\theta} = \arg\max_{\theta} L(\theta|X)\]
Dabei wird oft die logarithmierte Likelihood-Funktion verwendet, da sie numerisch stabiler ist und die Optimierung vereinfacht. Die logarithmierte Likelihood-Funktion lautet:
\[\log L(\theta|X) = \sum_{i=1}^n \log P(x_i|\theta)\]
Die Verwendung der logarithmierten Likelihood hat mehrere wichtige mathematische Vorteile:
Aus diesen Gründen wird in vielen Maschinelles Lernen-Algorithmen, einschließlich Tiefenlernens, die logarithmierte Likelihood zur Optimierung verwendet.
Die Maximum-Likelihood-Schätzung wird im Tiefenlernen wie folgt eingesetzt: 1. Modelltraining: Der Prozess des Minimierens der Verlustfunktion beim Lernen der Gewichte eines Neuronalen Netzes ist praktisch identisch mit der Maximum-Likelihood-Schätzung. 2. Wahrscheinlichkeitsmodellierung: Wird bei generativen Modellen zur Schätzung der Verteilung von Daten verwendet. 3. Hyperparameter-Tuning: Kann bei der Auswahl der Hyperparameter eines Modells eingesetzt werden.
Der bayessche Satz und die Maximum-Likelihood-Schätzung sind eng miteinander verwandt. Bei einer uniformen Prior-Verteilung im bayesschen Schätzverfahren ist die Maximum-a-posteriori (MAP)-Schätzung identisch mit der Maximum-Likelihood-Schätzung. Mathematisch ausgedrückt bedeutet dies, dass \(P(\theta|X) \propto P(X|\theta)P(\theta)\) bei einer konstanten \(P(\theta)\) zu \(\operatorname{argmax}_{\theta} P(\theta|X) = \operatorname{argmax}_{\theta} P(X|\theta)P(\theta)\) wird. Dies bedeutet, dass, wenn die Prior-Verteilung keine zusätzliche Information über den Parameter liefert, die Schätzung basierend nur auf den Daten (MLE) mit der bayesschen Schätzung (MAP) übereinstimmt.
Diese Konzepte sind essentiell für das Verständnis und die Optimierung des Trainings- und Inferenzprozesses in tiefen Lernmodellen. Im nächsten Abschnitt werden wir die Grundlagen der Informationstheorie besprechen.
Die MLE ist eine Methode, um den Parameter zu finden, der die gegebenen Daten am besten erklärt. Es geht darum, den Parameterwert zu finden, der die Likelihood (Wahrscheinlichkeit) der beobachteten Daten maximiert.
Likelihood-Funktion:
Log-Likelihood-Funktion:
Prozedur zur Berechnung der MLE:
Konkretes Beispiel:
MAP: Basierend auf dem Bayes’schen Theorem, wird die a-posteriori-Wahrscheinlichkeit durch Kombination von A-priori-Wahrscheinlichkeiten und Likelihood maximiert.
MAP-Schätzung: \[ \hat{\theta}_{MAP} = \arg\max_{\theta} p(\theta|x) = \arg\max_{\theta} \frac{p(x|\theta)p(\theta)}{p(x)} = \arg\max_{\theta} p(x|\theta)p(\theta) \]
MLE vs. MAP: | Eigenschaft | MLE | MAP | | ——————— | ——————————————————————– | ———————————————————————- | | Grundlage | frequentistisch (Frequentist) | bayesianisch (Bayesian) | | Ziel | Likelihood-Maximierung | Posterior-Wahrscheinlichkeitsmaximierung | | Prior-Wahrscheinlichkeit | nicht berücksichtigt | berücksichtigt | | Ergebnis | Punktenschätzung (Point Estimate) | Punktenschätzung (generell) oder Verteilungsschätzung (bei bayesianischer Inferenz) | | Überanpassung | hohe Überanpassungsneigung | durch Prior-Wahrscheinlichkeit Überanpassung vermeidbar (z.B., Regularisierungseffekt) | | Rechenkomplexität | in der Regel gering | je nach Prior-Wahrscheinlichkeit kann die Komplexität zunehmen (insbesondere, wenn keine konjugierte Prior-Verteilung vorliegt) |
Einfluss von Prior-Wahrscheinlichkeiten:
Herausforderung: Wie kann die Menge an Informationen gemessen und Unsicherheit quantifiziert werden?
Frust des Forschers: Claude Shannon stand vor grundlegenden Fragen zur effizienten Übertragung und Kompression von Informationen in Kommunikationssystemen. Es war notwendig, eine theoretische Grundlage zu schaffen, um Informationen zu quantifizieren, festzulegen, wie stark Daten ohne Informationsverlust komprimiert werden können, und zu bestimmen, wie viel Information über einen verrauschten Kanal stabil übertragen werden kann.
Die Informationstheorie ist eine mathematische Theorie zur Kompression, Übertragung und Speicherung von Daten und spielt in der Bewertung und Optimierung des Leistungspotenzials von Modellen im Deep Learning eine wichtige Rolle. In diesem Abschnitt werden wir die grundlegenden Konzepte der Informationstheorie wie Entropie, gegenseitige Informationsmenge und KL-Divergenz erläutern.
Die Entropie ist ein Maß für die Unsicherheit von Informationen. Die Entropie H(P) einer Wahrscheinlichkeitsverteilung P wird folgendermaßen definiert:
\[H(P) = -\sum_{x} P(x) \log P(x)\]
Hierbei steht x für alle möglichen Ereignisse. Die wichtigsten Eigenschaften der Entropie sind die folgenden:
In der Deep Learning wird die Entropie hauptsächlich als Grundlage für die Kreuzentropie verwendet, die häufig als Verlustfunktion in Klassifikationsproblemen eingesetzt wird. Das folgende Beispiel berechnet die Entropie verschiedener Wahrscheinlichkeitsverteilungen und visualisiert die Entropie einer binären Verteilung.
from dldna.chapter_02.information_theory import calculate_entropy
calculate_entropy()Entropy of fair coin: 0.69
Entropy of biased coin: 0.33
Entropy of fair die: 1.39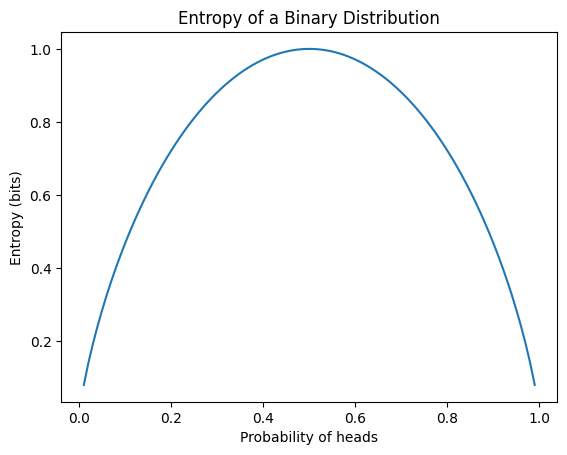
Die gegenseitige Information (Mutual Information) misst die Abhängigkeit zwischen zwei Zufallsvariablen X und Y. Mathematisch wird sie wie folgt definiert.
\[I(X;Y) = \sum_{x}\sum_{y} P(x,y) \log \frac{P(x,y)}{P(x)P(y)}\]
Die wesentlichen Eigenschaften der gegenseitigen Information sind:
Die gegenseitige Information wird in verschiedenen maschinellen Lernaufgaben wie Merkmalsauswahl und Dimensionsreduktion eingesetzt. Das folgende Beispiel zeigt die Berechnung und Visualisierung der gegenseitigen Information für eine einfache gemeinsame Wahrscheinlichkeitsverteilung.
from dldna.chapter_02.information_theory import mutual_information_example
mutual_information_example()Mutual Information: 0.0058
Die KL-Divergenz (Kullback-Leibler) ist eine Methode, um die Differenz zwischen zwei Wahrscheinlichkeitsverteilungen P und Q zu messen. Die KL-Divergenz von Q bezüglich P wird wie folgt definiert.
\[D_{KL}(P||Q) = \sum_{x} P(x) \log \frac{P(x)}{Q(x)}\]
Die wichtigsten Eigenschaften der KL-Divergenz sind:
Die KL-Divergenz wird in Deep Learning auf folgende Weise eingesetzt:
Konzepte der Informationstheorie sind eng miteinander verbunden. Zum Beispiel kann die gegenseitige Informationsmenge als Differenz von Entropie und bedingter Entropie ausgedrückt werden.
\(I(X;Y) = H(X) - H(X|Y)\)
Des Weiteren kann die KL-Divergenz als Differenz zwischen Kreuzentropie und Entropie dargestellt werden.
\(D_{KL}(P||Q) = H(P,Q) - H(P)\)
Hierbei ist \(H(P,Q)\) die Kreuzentropie von \(P\) und \(Q\). Im Folgenden wird die KL-Divergenz zwischen zwei Wahrscheinlichkeitsverteilungen berechnet und die Verteilungen visualisiert.
from dldna.chapter_02.information_theory import kl_divergence_example
kl_divergence_example()KL(P||Q): 0.0823
KL(Q||P): 0.0872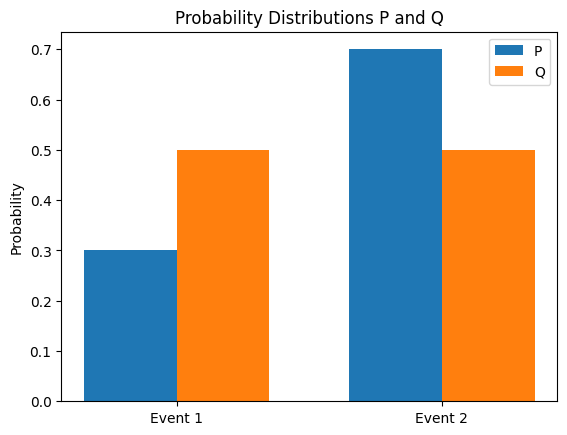
Diese Konzepte der Informationstheorie werden weitgehend bei der Gestaltung und Optimierung von Deep-Learning-Modellen angewendet. Zum Beispiel wird eine Kombination aus Rekonstruktionsfehler und KL-Divergenz als Verlustfunktion in Autoencodern verwendet, oder die KL-Divergenz dient als Nebenbedingung für die Richtlinienoptimierung im Reinforcement Learning.
Im nächsten Kapitel werden wir untersuchen, wie diese Konzepte der Wahrscheinlichkeit, Statistik und Informationstheorie in realen Deep-Learning-Modellen angewendet werden.
Definition: Die Informationsmenge (Information Content, Selbstinformation) stellt die Menge der Information dar, die bei dem Eintreten eines bestimmten Ereignisses gewonnen wird. Je seltener ein Ereignis auftritt, desto höher ist seine Informationsmenge.
Formel: \[I(x) = -\log(P(x))\]
Intuitiver Erklärung:
Eigenschaften:
Definition: Die Kreuzentropie (Cross Entropy) ist ein Maß für die Differenz zwischen zwei Wahrscheinlichkeitsverteilungen \(P\) und \(Q\). Wenn \(P\) die wahre Verteilung und \(Q\) die geschätzte Verteilung ist, repräsentiert die Kreuzentropie die durchschnittliche Anzahl von Bits, die benötigt werden, um die Wahre Verteilung \(P\) mit der geschätzten Verteilung \(Q\) darzustellen.
Herleitung:
Intuitiver Erklärung:
Binary Cross Entropy (BCE):
Categorical Cross Entropy (CCE):
KL-Divergence (Kullback-Leibler Divergence):
Beziehung zwischen KL-Divergence und Cross Entropy:
\[D_{KL}(P||Q) = \sum_{x} P(x) \log P(x) - \sum_{x} P(x) \log Q(x) = -\sum_{x} P(x) \log Q(x) - (-\sum_{x} P(x) \log P(x))\] \[D_{KL}(P||Q) = H(P, Q) - H(P)\]
\(H(P,Q)\): Cross Entropy
\(H(P)\): Entropie
Die KL-Divergence ist der Wert von Cross Entropy minus die Entropie von \(P\).
Wenn \(P\) fixiert ist, entspricht das Minimieren von Cross Entropy dem Minimieren von KL-Divergence.
Mutual Information (MI) (gemeinsame Informationsmenge):
Bedingte Entropie ( konditionale Entropie ):
Beziehung zwischen gegenseitiger Information und bedingter Entropie: \[I(X;Y) = H(X) - H(X|Y) = H(Y) - H(Y|X)\]
Die Verlustfunktion (Loss Function) ist eine Funktion, die das Maß der Abweichung zwischen den Vorhersagen eines maschinellen Lernmodells und den tatsächlichen Werten misst. Das Ziel des Modelltrainings besteht darin, die Parameter (Gewichte und Bias) zu finden, die den Wert dieser Verlustfunktion minimieren. Die Wahl einer geeigneten Verlustfunktion hat einen großen Einfluss auf die Leistung des Modells, daher muss sie sorgfältig basierend auf dem Problemtyp und den Eigenschaften der Daten ausgewählt werden.
Im Allgemeinen kann die Verlustfunktion \(L\) mit den Parametern \(\theta\), Datenpunkten \((x_i, y_i)\) wie folgt dargestellt werden. (Hierbei ist \(y_i\) der tatsächliche Wert und \(f(x_i; \theta)\) der vorhergesagte Wert des Modells)
\(L(\theta) = \frac{1}{N} \sum_{i=1}^{N} l(y_i, f(x_i; \theta))\)
\(N\) ist die Anzahl der Datenpunkte, \(l\) ist die Funktion (Loss Term), die den Verlust für einzelne Datenpunkte darstellt.
Die folgenden Verlustfunktionen werden häufig in maschinellem Lernen und Deep Learning verwendet.
Das Lernen vieler maschineller Modelle kann aus der Perspektive des Maximum Likelihood Estimations (MLE) erklärt werden. MLE ist eine Methode, um die Modellparameter zu finden, die die gegebenen Daten am besten erklären. Unter der Annahme, dass die Daten unabhängig und identisch verteilt (i.i.d.) sind, wird die Likelihood-Funktion wie folgt definiert:
\(L(\theta) = P(D|\theta) = \prod_{i=1}^{N} P(y_i | x_i; \theta)\)
Hier ist \(D = \{(x_1, y_1), (x_2, y_2), ..., (x_N, y_N)\}\) das Trainingsdatensatz, \(\theta\) sind die Modellparameter. \(P(y_i | x_i; \theta)\) ist die Wahrscheinlichkeit (oder Dichte) dafür, dass das Modell bei Eingabe von \(x_i\) den Ausgang \(y_i\) produziert.
Das Ziel der MLE ist es, den Parameter \(\theta\) zu finden, der die Likelihood-Funktion \(L(\theta)\) maximiert. In der Praxis ist es berechnungstechnisch einfacher, die log-Likelihood-Funktion zu maximieren.
\(\log L(\theta) = \sum_{i=1}^{N} \log P(y_i | x_i; \theta)\)
MSE und MLE: Bei einem linearen Regressionsmodell, bei dem angenommen wird, dass die Fehler einer Normalverteilung mit Mittelwert 0 und Varianz \(\sigma^2\) folgen, ist das Minimieren des MSE äquivalent zum Maximum Likelihood Estimation (MLE).
\(P(y_i | x_i; \theta) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(y_i - f(x_i; \theta))^2}{2\sigma^2}\right)\)
Die log-Likelihood-Funktion lautet wie folgt: \(\log L(\theta) = -\frac{N}{2}\log(2\pi\sigma^2) - \frac{1}{2\sigma^2}\sum_{i=1}^{N}(y_i - f(x_i;\theta))^2\)
Unter Berücksichtigung von Konstanten und der Annahme, dass \(\sigma^2\) eine Konstante ist, entspricht das Maximieren der log-Likelihood dem Minimieren des MSE.
Cross-Entropy und MLE: Bei Klassifikationsproblemen können die Ausgänge \(\hat{y}_i\) als Parameter einer Bernoulli-Verteilung (binäre Klassifikation) oder einer Multinomialverteilung (mehrklassige Klassifikation) interpretiert werden. In diesem Fall entspricht das MLE dem Minimieren des Cross-Entropy Loss.
Binäre Klassifikation (Bernoulli-Verteilung): Angenommen, \(\hat{y_i}\) ist die von dem Modell vorhergesagte Wahrscheinlichkeit dafür, dass \(y_i=1\) ist, \(P(y_i|x_i;\theta) = \hat{y_i}^{y_i} (1 - \hat{y_i})^{(1-y_i)}\) log-Likelihood: \(\log L(\theta) = \sum_{i=1}^{N} [y_i \log(\hat{y}_i) + (1 - y_i)\log(1 - \hat{y}_i)]\)
Mehrklassige Klassifikation (Categorical/Multinoulli-Verteilung): \(P(y_i | x_i; \theta) = \prod_{j=1}^{C} \hat{y}_{ij}^{y_{ij}}\) (one-hot Kodierung) log-Likelihood: \(\log L(\theta) = \sum_{i=1}^N \sum_{j=1}^C y_{ij} \log(\hat{y}_{ij})\)
Daher entspricht das Minimieren des Cross-Entropy Loss dem Prozess des Maximum Likelihood Estimations (MLE), um die Parameter zu finden, die die Verteilung der Daten am besten modellieren.
Kullback-Leibler Divergenz (KLD):
Beschreibung: Maßt den Unterschied zwischen zwei Wahrscheinlichkeitsverteilungen P und Q. P stellt die Verteilung der echten Daten dar, Q die vom Modell geschätzte Verteilung.
Focal Loss:
Huber Loss: Eine Verlustfunktion, die die Vorteile von MSE und MAE kombiniert. Für Fehler unter einem bestimmten Wert (\(\delta\)) wird quadratischer Fehler verwendet, ähnlich wie bei MSE, für größere Fehler wird absoluter Fehler verwendet, ähnlich wie bei MAE. Es ist robust gegenüber Ausreißern und differenzierbar.
\(L_\delta(y, \hat{y}) = \begin{cases} \frac{1}{2}(y - \hat{y})^2 & \text{wenn } |y - \hat{y}| \le \delta \\ \delta(|y - \hat{y}| - \frac{1}{2}\delta) & \text{sonst} \end{cases}\)
Log-Cosh Loss: Definiert als \(\log(\cosh(y - \hat{y}))\). Ähnlich wie Huber Loss ist es robust gegenüber Ausreißern und hat den Vorteil, an allen Punkten zweimal differenzierbar zu sein.
Quantil Loss: Wird verwendet, um die Vorhersagefehler an einem bestimmten Quantil zu minimieren.
Contrastive Loss, Triplet Loss: Wird in Siamese Networks und Triplet Networks verwendet, um die Distanz zwischen ähnlichen Sample-Paaren/Drillingen zu regulieren. (Siehe detaillierte Informationen in relevanten Publikationen)
Connectionist Temporal Classification (CTC) Loss: Wird in Fällen verwendet, in denen die Ausrichtung (Alignment) zwischen Eingabe- und Ausgabe-Sequenzen bei Aufgaben wie Spracherkennung und Handschrifterkennung nicht eindeutig ist.
Verlustfunktionen sind ein wichtiger Faktor, der die Leistung von Deep-Learning-Modellen beeinflusst. Es wird von Deep-Learning-Entwicklern verlangt, basierend auf den Eigenschaften des Problems, der Verteilung der Daten und der Struktur des Modells geeignete Verlustfunktionen auszuwählen und gegebenenfalls neue Verlustfunktionen zu entwickeln.
Bestehende Verlustfunktionen (MSE, Cross-Entropy usw.) sind nicht immer die optimale Wahl. Abhängig von den speziellen Anforderungen des Problems, der Verteilung der Daten und der Struktur des Modells kann es notwendig sein, neue Verlustfunktionen zu entwerfen. Der Entwurf neuer Verlustfunktionen ist ein wichtiger Teil der Deep-Learning-Forschung und hat das Potenzial, die Leistung des Modells erheblich zu verbessern.
Beim Entwurf neuer Verlustfunktionen sollten folgende Prinzipien beachtet werden:
Problemdefinition und Ziel: Das zu lösende Problem und das ultimative Ziel des Modells müssen klar definiert sein. Die Verlustfunktion ist ein zentrales Element, das bestimmt, was das Modell lernen soll (z. B. lediglich die Klassifikationsgenauigkeit erhöhen, bestimmte Klassen besser treffen, False Positive/False Negative-Raten regulieren usw.).
Mathematische Gültigkeit:
Interpretierbarkeit (Interpretability): Eine intuitive Verständlichkeit der Bedeutung der Verlustfunktion hilft bei der Analyse und Debugging des Lernprozesses. Jeder Term sollte klar definiert sein, was er bewirkt und welche Bedeutung er hat. Die Bedeutung und der Einfluss von Hyperparametern sollten ebenfalls klar sein.
Recheneffizienz (Computational Efficiency): Da die Verlustfunktion bei jeder Iteration und für alle (oder Minibatches) Datenpunkte berechnet wird, kann ein hoher Rechenaufwand das Lern Tempo verlangsamen.
Modifikation/Kombination bestehender Verlustfunktionen:
Entwurf basierend auf probabilistischen Modellen:
Entwurf von problembezogenen Verlustfunktionen:
Das Design von neuen Verlustfunktionen ist ein kreativer Prozess, der gleichzeitig eine vorsichtige Herangehensweise erfordert. Es ist wichtig, das Wesen des Problems tief zu verstehen, auf mathematischen/statistischen Prinzipien basierend zu gestalten und durch gründliche Experimente die Leistung zu überprüfen.
In diesem Kapitel haben wir die mathematischen Grundlagen des Deep Learnings betrachtet. Wir haben gesehen, wie Konzepte aus verschiedenen Bereichen wie lineare Algebra, Analysis, Wahrscheinlichkeit und Statistik sowie Informationstheorie bei der Gestaltung, dem Lernen und der Analyse von Deep Learning-Modellen eingesetzt werden. Diese mathematischen Werkzeuge sind essentiell, um komplexe neuronale Netzstrukturen zu verstehen, effiziente Lernalgorithmen zu entwickeln, die Leistung von Modellen zu bewerten und zu verbessern. Sie spielen auch eine wichtige Rolle bei der Suche nach neuen Durchbrüchen an der Frontlinie der Deep Learning-Forschung.
Berechnen Sie das Skalarprodukt (dot product) der beiden Vektoren \(\mathbf{a} = \begin{bmatrix} 1 \\ 2 \end{bmatrix}\) und \(\mathbf{b} = \begin{bmatrix} 3 \\ 4 \end{bmatrix}\).
Berechnen Sie das Produkt \(\mathbf{Ab}\) der Matrix \(\mathbf{A} = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}\) und des Vektors \(\mathbf{b} = \begin{bmatrix} 5 \\ 6 \end{bmatrix}\).
Erzeugen Sie eine 2x2 Einheitsmatrix (identity matrix).
Schreiben Sie die Definition der L1-Norm und der L2-Norm eines Vektors auf, und berechnen Sie die L1-Norm und die L2-Norm des Vektors \(\mathbf{v} = \begin{bmatrix} 3 \\ -4 \end{bmatrix}\).
Bestimmen Sie die Eigenwerte (eigenvalue) und die Eigenvektoren (eigenvector) der Matrix \(\mathbf{A} = \begin{bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix}\).
Überprüfen Sie, ob die inverse Matrix zu einer gegebenen Matrix existiert, und berechnen Sie sie, falls sie existiert. \(\mathbf{A} = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}\)
Erklären Sie, wie die Basisvektoren \(\mathbf{e_1} = \begin{bmatrix} 1 \\ 0 \end{bmatrix}\) und \(\mathbf{e_2} = \begin{bmatrix} 0 \\ 1 \end{bmatrix}\) unter der linearen Transformation \(T(\mathbf{x}) = \mathbf{Ax}\) transformiert werden, und visualisieren Sie die Ergebnisse. (Gegeben ist \(\mathbf{A} = \begin{bmatrix} 2 & -1 \\ 1 & 1 \end{bmatrix}\))
Berechnen Sie den Rang (rank) der folgenden Matrix. \(\mathbf{A} = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix}\)
Schreiben Sie die Definition der Singulärwertzerlegung (Singular Value Decomposition, SVD) auf und führen Sie eine SVD für die gegebene Matrix \(\mathbf{A}\) durch. \(\mathbf{A} = \begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{bmatrix}\)
Erklären Sie das Ziel und den Prozess der Hauptkomponentenanalyse (Principal Component Analysis, PCA) und führen Sie eine PCA für ein gegebenes Datenset durch, um die Dimension auf eins zu reduzieren.
import numpy as np
data = np.array([[1, 2], [2, 3], [3, 4], [4, 5], [5, 6]])Bestimmen Sie eine Basis für den Nullraum (null space) und den Spaltenraum (column space) der folgenden Matrix. \(\mathbf{A} = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix}\)
Schreiben Sie die Definition der QR-Zerlegung auf und führen Sie eine QR-Zerlegung für die gegebene Matrix \(\mathbf{A}\) durch. (Die QR-Zerlegung ist ein numerisch stabiles Verfahren, das zum Lösen linearer Gleichungssysteme oder zur Lösung von Eigenwertproblemen verwendet wird.) \(\mathbf{A} = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}\)
Skalarprodukt: \(\mathbf{a} \cdot \mathbf{b} = (1)(3) + (2)(4) = 3 + 8 = 11\)
Matrix-Vektor Produkt: \(\mathbf{Ab} = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \begin{bmatrix} 5 \\ 6 \end{bmatrix} = \begin{bmatrix} (1)(5) + (2)(6) \\ (3)(5) + (4)(6) \end{bmatrix} = \begin{bmatrix} 17 \\ 39 \end{bmatrix}\)
2x2 Einheitsmatrix: \(\mathbf{I} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\)
L1, L2 Norm:
\(\mathbf{v} = \begin{bmatrix} 3 \\ -4 \end{bmatrix}\) \(||\mathbf{v}||_1 = |3| + |-4| = 3 + 4 = 7\) \(||\mathbf{v}||_2 = \sqrt{(3)^2 + (-4)^2} = \sqrt{9 + 16} = \sqrt{25} = 5\)
Eigenwerte, Eigenvektoren: \(\mathbf{A} = \begin{bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix}\)
Charakteristische Gleichung: \(\det(\mathbf{A} - \lambda\mathbf{I}) = 0\) \((2-\lambda)^2 - (1)(1) = 0\) \(\lambda^2 - 4\lambda + 3 = 0\) \((\lambda - 3)(\lambda - 1) = 0\) \(\lambda_1 = 3\), \(\lambda_2 = 1\)
Eigenvektor (λ = 3): \((\mathbf{A} - 3\mathbf{I})\mathbf{v} = 0\) \(\begin{bmatrix} -1 & 1 \\ 1 & -1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix}\) \(x = y\), \(\mathbf{v_1} = \begin{bmatrix} 1 \\ 1 \end{bmatrix}\) (oder ein beliebiges Vielfaches davon)
Eigenvektor (λ = 1): \((\mathbf{A} - \mathbf{I})\mathbf{v} = 0\) \(\begin{bmatrix} 1 & 1 \\ 1 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix}\) \(x = -y\), \(\mathbf{v_2} = \begin{bmatrix} -1 \\ 1 \end{bmatrix}\) (oder ein beliebiges Vielfaches davon)
Inverse Matrix: \(\mathbf{A} = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}\)
SVD: \(\mathbf{A} = \mathbf{U\Sigma V^T}\)
(Berechnungsprozess wird hier nicht dargestellt. Berechnung mit Bibliotheken wie NumPy möglich: U, S, V = np.linalg.svd(A))
PCA:
import numpy as np
data = np.array([[1, 2], [2, 3], [3, 4], [4, 5], [5, 6]])
# 1. Datenzentrierung (Mittelwert abziehen)
mean = np.mean(data, axis=0)
centered_data = data - mean
# 2. Kovarianzmatrix berechnen
covariance_matrix = np.cov(centered_data.T)
# 3. Eigenwerte und Eigenvektoren berechnen
eigenvalues, eigenvectors = np.linalg.eig(covariance_matrix)
# 4. Hauptkomponente auswählen (Eigenvektor zum größten Eigenwert)
# Eigenwerte in absteigender Reihenfolge sortieren und den Eigenvektor zum größten Eigenwert auswählen
sorted_indices = np.argsort(eigenvalues)[::-1] # Indizes in absteigender Reihenfolge sortieren
largest_eigenvector = eigenvectors[:, sorted_indices[0]]projected_data = centered_data.dot(largest_eigenvector)
print(projected_data)
3. **Nullraum, Spaltenraum Basen:**
$\mathbf{A} = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix}$
* **Nullraum (Null Space):** Finden von $\mathbf{x}$, die $\mathbf{Ax} = 0$ erfüllt.
Durch Umwandlung in Zeilenstufenform kann die Lösung gefunden werden:
$\mathbf{x} = t\begin{bmatrix} 1 \\ -2 \\ 1 \end{bmatrix}$ (wobei $t$ eine beliebige Konstante ist).
Daher ist die Basis des Nullraums $\begin{bmatrix} 1 \\ -2 \\ 1 \end{bmatrix}$.
* **Spaltenraum (Column Space):** Der Raum, der durch Linearkombinationen der Spaltenvektoren von Matrix $\mathbf{A}$ erzeugt wird.
Die Spaltenvektoren der ursprünglichen Matrix, die den Pivot-Spalten in der Zeilenstufenform entsprechen, bilden die Basis:
$\begin{bmatrix} 1 \\ 4 \\ 7 \end{bmatrix}$, $\begin{bmatrix} 2 \\ 5 \\ 8 \end{bmatrix}$
4. **QR-Zerlegung:**
$\mathbf{A} = \mathbf{QR}$
* $\mathbf{Q}$: Matrix mit orthonormalen Spaltenvektoren
* $\mathbf{R}$: obere Dreiecksmatrix (upper triangular matrix)
(Das Berechnungsverfahren kann das Gram-Schmidt-Verfahren zur Orthogonalisierung verwenden oder eine Bibliothek wie NumPy, z.B. `Q, R = np.linalg.qr(A)`)
:::
## Übungen
### 2 Analysis und Optimierung
#### Grundlagen
1. Bestimmen Sie die Ableitungsfunktion $f'(x)$ von $f(x) = x^3 - 6x^2 + 9x + 1$.
2. Bestimmen Sie die partiellen Ableitungen $\frac{\partial f}{\partial x}$ und $\frac{\partial f}{\partial y}$ der Funktion $f(x, y) = x^2y + 2xy^2$.
3. Bestimmen Sie die Ableitungsfunktion $f'(x)$ von $f(x) = \sin(x^2)$ unter Verwendung der Kettenregel.
#### Anwendungen
1. Bestimmen Sie den Gradienten $\nabla f$ der Funktion $f(x, y) = e^{x^2 + y^2}$ und berechnen Sie dessen Wert im Punkt (1, 1).
2. Finden Sie alle kritischen Punkte der Funktion $f(x) = x^4 - 4x^3 + 4x^2$ und klassifizieren Sie jeden als lokales Maximum, Minimum oder Sattelpunkt.
3. Bestimmen Sie die Jacobimatrix der folgenden Funktion:
$f(x, y) = \begin{bmatrix} x^2 + y^2 \\ 2xy \end{bmatrix}$
#### Vertiefung
1. Verwenden Sie die Lagrange-Multiplikatoren-Methode, um das Maximum und Minimum der Funktion $f(x, y) = xy$ unter der Nebenbedingung $g(x, y) = x^2 + y^2 - 1 = 0$ zu bestimmen.
2. Verwenden Sie die Gradientenabstiegs-Methode (Gradient Descent), um das Minimum der Funktion $f(x) = x^4 - 4x^3 + 4x^2$ zu finden. (Startwert: $x_0 = 3$, Lernrate: $\alpha = 0.01$, Anzahl der Iterationen: 100)
3. Drücken Sie den Gradienten $\nabla f$ der Funktion $f(\mathbf{x}) = \mathbf{x}^T \mathbf{A} \mathbf{x}$ mit Hilfe von $\mathbf{A}$ und $\mathbf{x}$ aus. (Dabei ist $\mathbf{A}$ eine symmetrische Matrix.)
4. Verwenden Sie die Newton-Methode, um die Nullstellen der Gleichung $x^3 - 2x - 5 = 0$ zu finden.
::: {.callout-note collapse="true" title="Klicken Sie hier, um den Inhalt anzuzeigen (Lösung)"}
## Übungen Lösungen
### 2 Differential- und Integralrechnung sowie Optimierung
#### Grundlagen
1. **Ableitung:**
$f(x) = x^3 - 6x^2 + 9x + 1$
$f'(x) = 3x^2 - 12x + 9$
2. **Partielle Ableitungen:**
$f(x, y) = x^2y + 2xy^2$
$\frac{\partial f}{\partial x} = 2xy + 2y^2$
$\frac{\partial f}{\partial y} = x^2 + 4xy$
3. **Kettenregel:**
$f(x) = \sin(x^2)$
$f'(x) = \cos(x^2) \cdot (2x) = 2x\cos(x^2)$
#### Anwendungen
1. **Gradient:**
$f(x, y) = e^{x^2 + y^2}$
$\nabla f = \begin{bmatrix} \frac{\partial f}{\partial x} \\ \frac{\partial f}{\partial y} \end{bmatrix} = \begin{bmatrix} 2xe^{x^2 + y^2} \\ 2ye^{x^2 + y^2} \end{bmatrix}$
$\nabla f(1, 1) = \begin{bmatrix} 2e^2 \\ 2e^2 \end{bmatrix}$
2. **Kritische Punkte und Extremwertbestimmung:**
$f(x) = x^4 - 4x^3 + 4x^2$
$f'(x) = 4x^3 - 12x^2 + 8x = 4x(x-1)(x-2)$
Kritische Punkte: $x = 0, 1, 2$
$f''(x) = 12x^2 - 24x + 8$
* $f''(0) = 8 > 0$: Tiefpunkt
* $f''(1) = -4 < 0$: Hochpunkt
* $f''(2) = 8 > 0$: Tiefpunkt
3. **Jacobian Matrix:**
$f(x, y) = \begin{bmatrix} x^2 + y^2 \\ 2xy \end{bmatrix}$
$\mathbf{J} = \begin{bmatrix} \frac{\partial f_1}{\partial x} & \frac{\partial f_1}{\partial y} \\ \frac{\partial f_2}{\partial x} & \frac{\partial f_2}{\partial y} \end{bmatrix} = \begin{bmatrix} 2x & 2y \\ 2y & 2x \end{bmatrix}$
#### Vertiefung
1. **Lagrange Multiplikatoren:**
$L(x, y, \lambda) = xy - \lambda(x^2 + y^2 - 1)$
$\frac{\partial L}{\partial x} = y - 2\lambda x = 0$
$\frac{\partial L}{\partial y} = x - 2\lambda y = 0$
$\frac{\partial L}{\partial \lambda} = x^2 + y^2 - 1 = 0$
* $x = \pm \frac{1}{\sqrt{2}}$, $y = \pm \frac{1}{\sqrt{2}}$, $\lambda = \pm \frac{1}{2}$
* Maximum: $f(\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}) = f(-\frac{1}{\sqrt{2}}, -\frac{1}{\sqrt{2}}) = \frac{1}{2}$
* Minimum: $f(\frac{1}{\sqrt{2}}, -\frac{1}{\sqrt{2}}) = f(-\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}) = -\frac{1}{2}$
2. **Gradientenabstieg:**
```python
def gradient_descent(f, df, x0, alpha, iterations):
x = x0
for i in range(iterations):
x = x - alpha * df(x)
return x
```
f = lambda x: x**4 - 4*x**3 + 4*x**2
df = lambda x: 4*x**3 - 12*x**2 + 8*x
x_min = gradient_descent(f, df, 3, 0.01, 100)
print(x_min) # konvergiert etwa bei 2Gradient (Matrixform): \(f(\mathbf{x}) = \mathbf{x}^T \mathbf{A} \mathbf{x}\) \(\nabla f = (\mathbf{A} + \mathbf{A}^T)\mathbf{x}\). Da \(\mathbf{A}\) eine symmetrische Matrix ist, gilt \(\nabla f = 2\mathbf{A}\mathbf{x}\)
Newton-Verfahren: \(f(x) = x^3 - 2x - 5\) \(f'(x) = 3x^2 - 2\) \(x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}\)
def newton_method(f, df, x0, iterations):
x = x0
for i in range(iterations):
x = x - f(x) / df(x)
return x
f = lambda x: x**3 - 2*x - 5
df = lambda x: 3*x**2 - 2
root = newton_method(f, df, 2, 5) # Startwert x0 = 2, 5 Iterationen
print(root)Berechnen Sie die Wahrscheinlichkeit, dass bei drei Münzwürfen zweimal Kopf erscheint.
Berechnen Sie die Wahrscheinlichkeit, dass eine gerade Zahl erscheint, wenn ein Würfel geworfen wird.
Schreiben Sie die Wahrscheinlichkeitsdichtefunktion (PDF) der Normalverteilung auf und erklären Sie den Begriff Mittelwert und Varianz.
Erklären Sie den Satz von Bayes (Bayes’ theorem) und wenden Sie ihn auf das folgende Problem an:
Erklären Sie das Konzept des Maximum-Likelihood-Schätzers (Maximum Likelihood Estimation, MLE) und bestimmen Sie den MLE für die Wahrscheinlichkeit, dass Kopf erscheint, wenn eine Münze fünfmal geworfen wird und dreimal Kopf erscheint.
Schreiben Sie die Definition des Erwartungswerts (expectation) auf und geben Sie die Formeln zur Berechnung des Erwartungswerts für diskrete und kontinuierliche Zufallsvariablen an.
Schreiben Sie die Definition der Entropie (entropy) auf und berechnen Sie die Entropie der folgenden Wahrscheinlichkeitsverteilung:
Angenommen, die gemeinsame Wahrscheinlichkeitsverteilung (joint probability distribution) von zwei Zufallsvariablen X und Y ist wie folgt gegeben, berechnen Sie dann die gegenseitige Information (mutual information) I(X;Y):
P(X=0, Y=0) = 0.1, P(X=0, Y=1) = 0.2
P(X=1, Y=0) = 0.3, P(X=1, Y=1) = 0.4Angenommen, die Wahrscheinlichkeitsverteilungen P und Q sind wie folgt gegeben, berechnen Sie dann die Kullback-Leibler-Divergenz \(D_{KL}(P||Q)\):
Schreiben Sie die Wahrscheinlichkeitsmassenfunktion (PMF) der Poisson-Verteilung auf und geben Sie ein Beispiel an, in welchen Fällen sie angewendet wird.
Münzwurf: Wahrscheinlichkeit = (Anzahl der Fälle, bei denen bei drei Würfen zweimal Kopf erscheint) * (Wahrscheinlichkeit für Kopf)^2 * (Wahrscheinlichkeit für Zahl)^1 = 3C2 * (1/2)^2 * (1/2)^1 = 3 * (1/4) * (1/2) = 3/8
Würfelwurf: Wahrscheinlichkeit = (Anzahl der Fälle, bei denen eine gerade Zahl erscheint) / (Gesamtanzahl der Fälle) = 3 / 6 = 1/2
Normalverteilung: \(f(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}\)
Bayes-Theorem: \(P(A|B) = \frac{P(B|A)P(A)}{P(B)}\)
\(P(A|B) = \frac{(0.99)(0.01)}{0.0198} = 0.5\) (50%)
Maximum Likelihood Schätzung (MLE):
Entropie: Entropie ist ein Maß für die Unsicherheit, Unordnung oder Informationsmenge in einer Wahrscheinlichkeitsverteilung. \(H(P) = -\sum_{x} P(x) \log P(x)\) (Die Basis des Logarithmus ist oft 2 oder der natürliche Logarithmus e)
\(H(P) = -(0.5 \log 0.5 + 0.25 \log 0.25 + 0.25 \log 0.25)\) (Bei Verwendung des logarithmischen Basisses 2) \(H(P) \approx 1.5\) Bits
Mutual Information: \(I(X;Y) = \sum_{x}\sum_{y} P(x,y) \log \frac{P(x,y)}{P(x)P(y)}\)
\(I(X;Y) = (0.1)\log\frac{0.1}{(0.3)(0.4)} + (0.2)\log\frac{0.2}{(0.3)(0.6)} + (0.3)\log\frac{0.3}{(0.7)(0.4)} + (0.4)\log\frac{0.4}{(0.7)(0.6)}\) \(I(X;Y) \approx 0.0867\) (bei Verwendung des logarithmischen Basisses 2)
KL-Divergenz: \(D_{KL}(P||Q) = \sum_{x} P(x) \log \frac{P(x)}{Q(x)}\) \(D_{KL}(P||Q) = 0.6 \log \frac{0.6}{0.8} + 0.4 \log \frac{0.4}{0.2} \approx 0.083\)
Poisson-Verteilung: